モノポリーにおける最も稼げる都市について数値計算[カード効果あり]

下記のモノポリーについての記事の続きです。
下記の記事では、実は「カード」の効果が考慮されていませんでした。

モノポリーでは、チャンスカードと共同基金カードの2種類があり、ゲームを左右する大きな効果があります。

今回はその効果も含めてた計算を行い、どの都市が最も稼げるのかを計算しました。

目的

今度はカード (チャンス、共同基金) の効果を入れて、計算してみた。

なおカードはそれぞれ 16 枚ずつある。

また前回のプログラム中では牢屋で足踏しているときに牢屋に止まった数には入れていなかったが、今回は足踏も、 入った数として計算する。

つまり牢屋で 2 回足踏をすれば、その分だけ牢屋に止まったと数えるのである。

モデル

今回のモデルを示す。

チャンスカード、共同基金カードの二種類のカードを予め適当に並べ、カードのマスに止まる度に次のカードを見て、その効果を反映する。

ただし今回反映したカードの効果は移動カードのみである。

つまり牢屋へ飛ぶとか、 3 マス戻るとか、その類。

ルール上使用したカードは即座にカードの山札の一番下に潜り込ませる。

そのため、今回初期のカードの順番 は適当にしたが、何周もすれば、どのカードをどこのマスで引くかはランダムになるはずで、初期のカード順は ほとんど影響しないはずである。

数値計算に使用したプログラムソース(fortran)

以下にソースを載せる。

コード内の「&lt;」は「<」と置き換えてください。

結果1

まずはカードがしっかり回っていることを示すために、プログラムを回し、カード番号を確かめる。

プログラム 中、カードには c1, c2 という変数をふっていて、この変数が 1 から始まり、一回カードを引くと 2 に変わり、次 第に増えて 16 まで来たら 1 に戻るようにしてある。

以下が結果である。

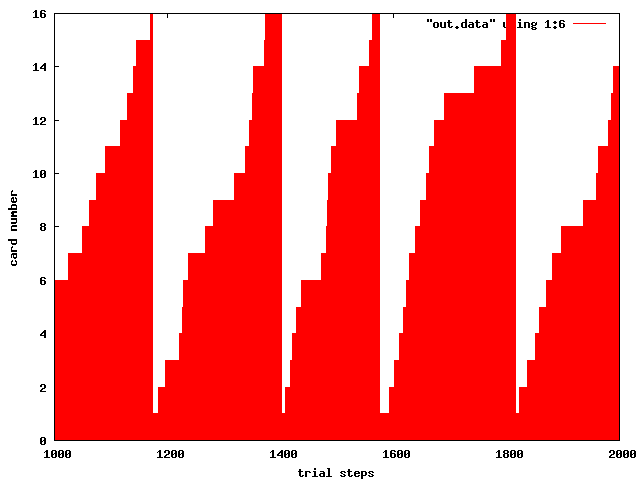
グラフからわかるように、おおよそ 200 回サイコロを振れば、使用したカードが一周 (つまり 16 枚使用) する。

この結果からカードはしっかり回っていることがわかる。

結果2

次にまた各都市を買うのに必要な費用をグラフにした。

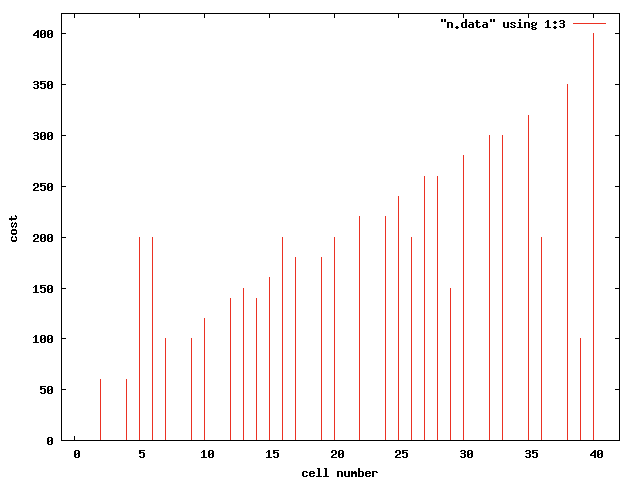
いよいよ以下に止まった数の計算結果を示す。

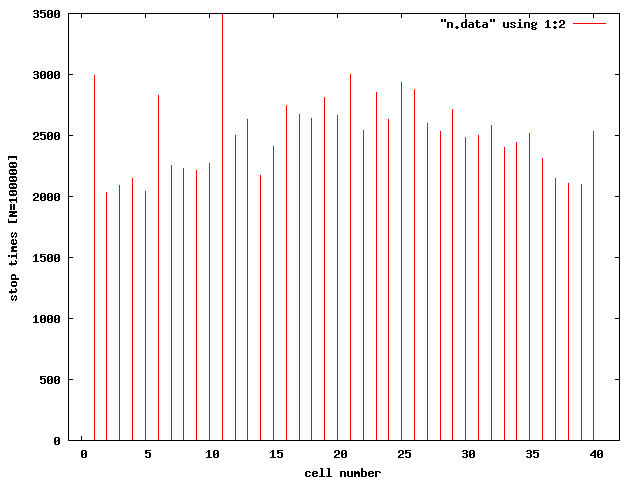
次に「期待値」を示す。この値が実質的に、その都市が持つ価値、儲かるかどうかを表した値となる。

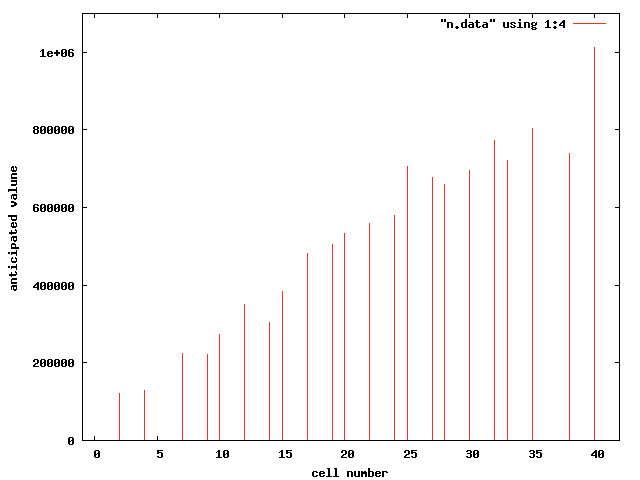
結果を見ると、明らかに右に行く方が儲かることがわかる。

これは止まる確率はどのマスも大して変わらない ために、初期投資金額の影響が出ている。

もっと詳しく見ていくと、「ボードウォークへ行く」というカードのお かげもあり、最後の都市ボードウォークの価値が高い。

ただ、その手前の都市の価値は低く、独占できたときには マスも多いグリーンの領域が儲かる可能性が高い。

他にはやはりカードの効果が効いて、イリノイの価値が周りより高い。