 たんたん
たんたんモノポリーって知ってる?



何それ?おいしいの?



いわゆるボードゲームの一つで、2-8人で遊ぶんだ。
ボード上の「都市」を買って、そこに止まった人からお金をとって行くゲーム
参加者同士での、都市の売買も自由で、交渉や戦術が問われるゲーム



へぇ〜



学生の頃は、徹夜でよくやっていたよ。



学生は勉強しろよ!



まぁまぁ
その時に、との「都市」を買っておくべきか、というのを真面目に計算したことがあったので、今回はそれを載せるよ。
目的
モノポリというボードゲームは 20 世紀初頭にアメリカ合衆国で生まれた。
プレイヤーはサイコロをふたつ振り、 出た目の数に応じて 40 個のマスを正方形の周囲を回るようにして回り、その途中途中で都市を買い、そのマスに 止まった他のプレイヤーから高額なレンタル料をとるゲームである。
このゲームの目的は自分以外のプレイヤー を破産に追い込むことである。
そこで重要なことが、限りある資金を使って、どの都市を買うか、もしくは交渉をし、手に入れるかである。
都市によって、買うために必要な費用も違えば、レンタル料も異なってくる。
そこで、 どの都市が一番儲かる都市なのかを計算することはモノポリをプレイする上では非常に大事なことである。
また モノポリ自体は政治や教育上の試みとして、製作された原型をもつ。
この原型からもわかるようにモノポリをプレイすることで、社会で生きていくために必要な、投資力、判断力、さらには交渉力が身につくと考える。
そこで今回は非常に簡単なモデルを提示し、そのモデル内でどの都市が最も儲かるかを計算した。
モデル
まず今回計算したモデルを示す。
モノポリには全部で 40 個のマスがあり、その内 22 マスが都市と呼ばれるマスである。
プレイヤー一人が「GO」 マスからサイコロをふたつ振り、40 個のマスを順々に巡り、41 マス目に「GO」に戻ってくるとする。これを何 周もする。(実際は計算上は数万周させた。)
ただし、毎回「GO」から始まるのではなく、「GO」マスを飛び越えての進みも可能である。
このときの各都市のマスに一体何回止まったかを計算する。
各都市において、相手プレイヤーから取れるレンタル料が、その都市の購入金額に比例すると仮定した。
この 仮定により、各都市に止まった回数に都市の購入金額を乗じた値が、すなわちその都市の「期待値」である。(こ こでは各都市間の比較をしたいだけなのでこの「期待値」が分かれば十分である。)
ただしここで注意したいのは、「GO TO JAIL」というマスである。このマスに止まると「JAIL」マスに戻って しまい。
保釈金を払うか、サイコロを振りゾロ目がでない限り最高 2 回足止めされる。
今回の計算では、簡単の ために、保釈金は払わないとして、「GO TO JAIL」に止まってしまった場合には、即時に「JAIL」に行き、サ イコロを振り、ゾロ目が出れば、その分だけ先に進む、出なければ最高 2 回まで足止めされるとした。
この仮定をしたことで、「GO TO JAIL」マス以降のマスは確率的に止まりにくいと考えられる。
数値計算に使用したプログラムソース(fortran)
下記に計算に使用したプログラムソースを示す。
program monopoly
implicit none
real ran, ran1, ran2
real d1, d2, d, s, m
integer i(3), seed, j, k, r
integer n(40), mon(40), seki
s=0.0
r=4
call itime(i) seed = i(3) * 131 ran= rand(seed)
do j=1, 40, 1
n(j) = 0
end do
open (1, file="out.data", status=’replace’)
open (3, file="ran.data", status=’replace’)
do j=0, 100000, 1
!ダイスを振る
ran = ran *1000.0 + 43.0 * real(j)**0.5
ran = rand(int(ran))
ran = ran *1000.0
ran1 = ran
d1 = mod(int(ran), 6) + 1 !一個目のダイス決定
ran = ran + 37.0 * real(j)**0.5
ran = rand(int(ran))
ran = ran *1000.0
ran2 = ran
d2 = mod(int(ran), 6) + 1 !二個目のダイス決定
d = d1 + d2
!ダイスを振った (d1, d2)。d はその合計、つまり進む数を決定
if (r>=2) then
s=s+d
m = mod(s, 40) + 1.0
n(int(m)) = n(int(m)) + 1
if (mod(m, 30)==0 ) then
s = s + 20.0
r=0
end if
!牢屋に入ってなければコマがどこに進んだかを計算。ただし変数型はreal
else if (d1 == d2) then !牢屋入っていれば、ゾロ目かどうかを判断
s = s + d !ゾロ目なら進む。
r = 2 !牢屋からもでる。
m = mod(s, 40) + 1.0
n(int(m)) = n(int(m)) + 1
if (mod(m, 30)==0 ) then
s = s + 20.0
r=0
end if
else !牢屋に入っていてかつゾロ目でなければ、進まずに牢屋に入った数を数える。
r=r+1
end if
write(1, "(2i10, 5f20.10)") j, r, d, s, m
write(3, "(i10, 2f20.10)") j, ran1, ran2
end do
close(3)
close(1)
open(10, file="mon.data", status=’old’)
do j=1, 40, 1
read(10,*) mon(j)
end do
close(10)
open(2, file="n.data", status=’replace’)
do j = 1, 40, 1
seki = n(j) * mon(j)
write(2, "(4i10)") j, n(j), mon(j), seki
end do
close(2)
end program monopoly
コード内の「<」は「<」と置き換えてください。
プログラムのポイント
このプログラムは変数 s をサイコロを振った分だけ進め、これを 40 で割って 1 足した数をそのときに止まった マスであるとした。
途中の if 分では「JAIL」に入っているかどうかの判断をし、結果に応じて処理(「JAIL」に 入ってないと判断されれば先に進む処理、そうでなければ進まないで「JAIL」に入ったときの回数計算処理、も しくはゾロ目が出ていれば「JAIL」から出て先に進む処理)を行う。
本プログラムで最も苦労した点は乱数の発生である。関数 rand() に時刻の秒数を入れて、乱数を発生させてい るが、全プログラムの計算時間は数秒しかないので、これだけでは同じ乱数が何度も発生してしまう。
そこで、初回に発生させた乱数を次の乱数の seed にした。
だが、それだけでは、実は乱数に周期的な波が出てきてしまった。 そこで次の乱数の seed にするときに do 文を回している変数 j の乗数 (0.5 乗) を seed の中にいれた。
こうするこ とで周期的な波を消した。
ここで 0.5 乗としたのには理由がある。それは j は 0 から 100000 まで回すために、例 えば 2 乗では最高で 10000000000 という数が出てきてしまい、どこかの変数がサチってしまう。
そこで j の乗数が最高でもあまり上がらないように、0.5 乗とした。
結果1
まずは乱数が少なくとも見ためでたしかに乱数っぽくなっているかどうかを確認する。
ここで χ2 検定などを使 用してその乱数っぷりを示してあげるのが筋であると思うが、眠いのでそれは割愛した。
発生させたサイコロの目の直前の乱数を以下に示す。
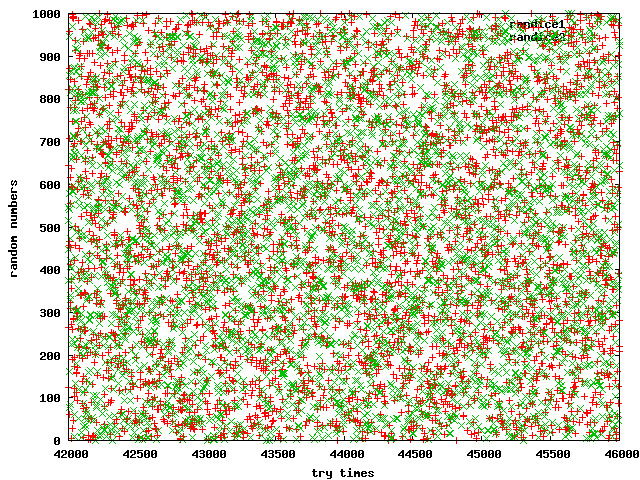

サイコロを振るのってこんなに苦労するんだなぁって思った。
結果2
次に本結果を示す。
その中でまずはどのマスにどれくらい止まったかの計算結果を示す。
なお乱数による効果の変化を見るために結果は二つ示す。
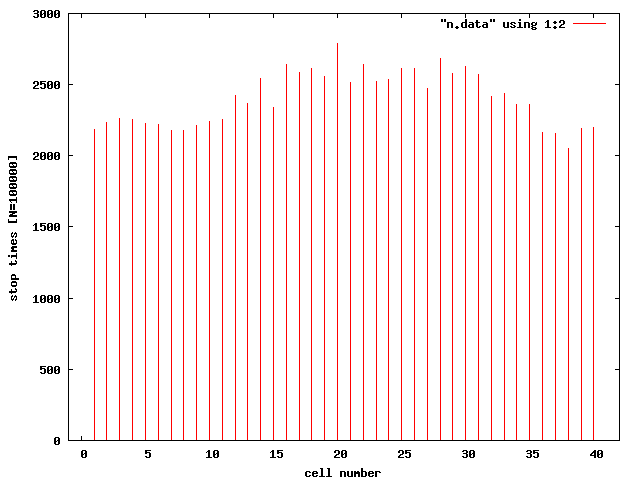

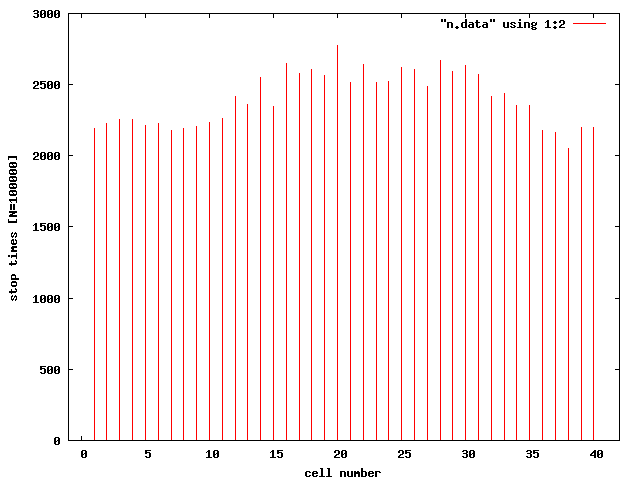

上記のグラフで横軸は各マスに振り分けられた番号。
1 番は「GO」、11 番は「JAIL」、21 番は「FREE PARK- ING」、31 番は「GO TO JAIL」である。
サイコロを振った数、つまり母数は 100000 回である。
次に「期待値」を示す前に、各都市を購入するための金額をグラフにした。
この値を上の値に乗じて「期待値」 を算出した。
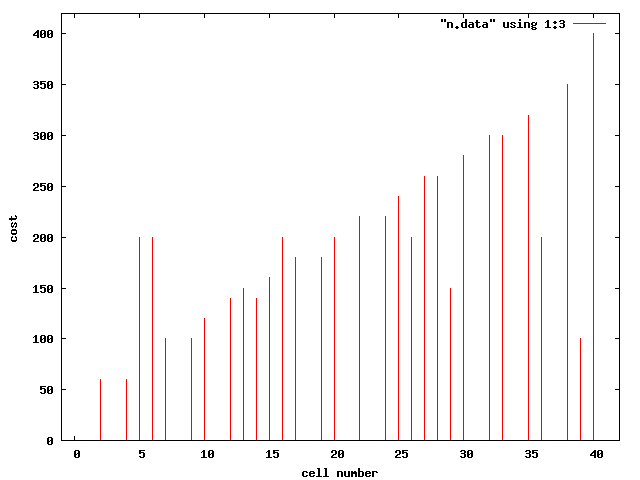

最後に「期待値」を示す。これがそれぞれの都市の価値だと考えてよい。
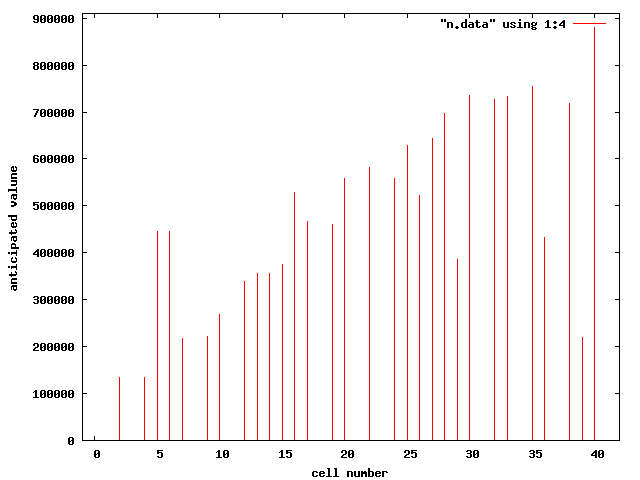

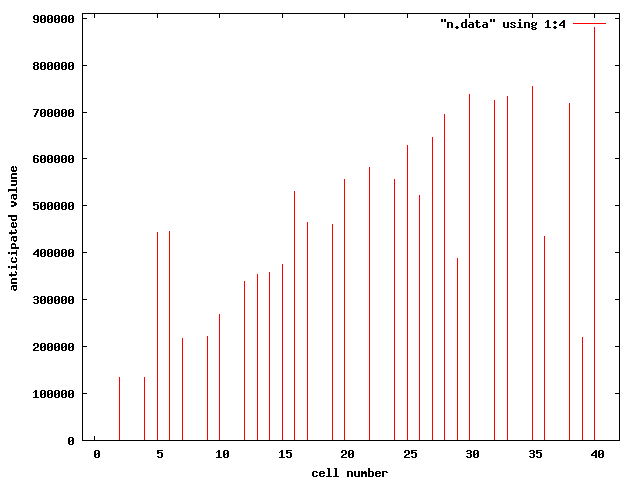

上記のグラフで縦軸の値そのものに特に意味はなく、その相対的な差に注目したい。
横軸は各マスに振り分け られた番号。1 番は「GO」、11 番は「JAIL」、21 番は「FREE PARKING」、31 番は「GO TO JAIL」である。
二回実行した結果を見比べて、乱数の不定性による結果の依存性は低いと考えられる。そこで以下に「期待値」 の結果をもっと大きく示す。
今度は都市以外は全て 0 にした。
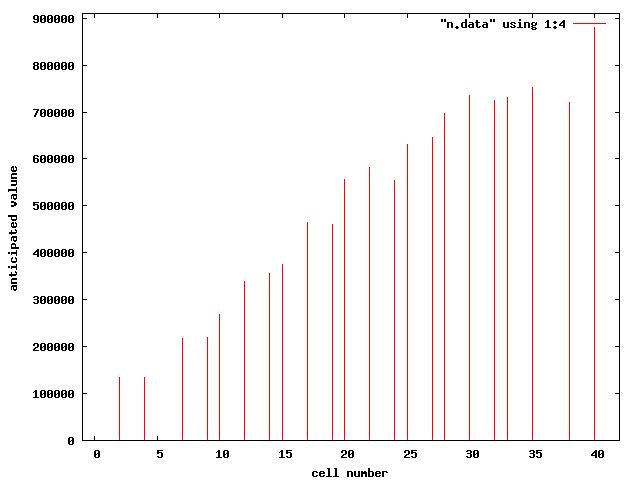

考察
まずは各マスの止まりやすさについて。
結果から見ると、cell number = 20 の「NEW YORK AVENUE:ニュー ヨーク通り」と cell number = 28 の「VENTNOR AVENUE:べントノール通り」を中心に二つ、もしくは三つの山になっていることがわかる。
さらに cell number = 31 の「GO TO JAIL」を堺にしてそれ以降、cell number = 11 の「JAIL」までは比較的低い。
これはまさに牢屋の効果である。
最終結果から、まず考えられるのは、右に行けば、行くほどに期待値が上がっていることである。
つまり基本 的には購入が高額な都市ほどに儲けも大きいということである。
ここからゲーム自体の設定として、各マスにお およそ同じ確率で止まるようになっていることが言える。
各都市の中でも特に目を引くのは最高額な都市 cell number = 40 の「BOARDWALK:ボードウォーク」である。
他の都市から飛び抜けて期待値が高い。
次に注目したいのはやはり、cell number = 32, 33, 35 の「PACIFIC AVENUE:パシフィッ ク通り、NORTH CAROLINA AVENUE:ノースキャロライナ通り、PENNSYLVANIA: ペンシルバニア通り」の地域である。
ここの三つの都市はともに、期待値が高く、ここを独占できれば、トップに立つ可能性が 高くなるだろう。
逆に目を引くのが cell number = 2, 4 の「MEDITER-RANEAN AVENUE:地中海通り、BALTIC AVENUE: バルティック通り」である。ここの地域は非常に期待値が低い。
以上では、各都市を購入するのに必要な経費を考慮にはいれておらず、上記にある考えでゲームを進めた場合 に勝てる確率は増えるとは考えられるが、確実というわけには行かない。
なぜなら序盤と終盤での各都市の発展 速度や、所持金の多少、交渉の成功失敗などは考慮していないからである。
それでもどのマスが止まりやすく、儲けやすいかを計算できた。


備考: cell numberと都市名
ここで上記の議論で使用した「cell number」と実際のモノポリーでの都市名・マス名を示しておく。
[wikpedia]
| 1 | GO |
| 2 | 地中海(メディタレーニアン)通り |
| 3 | 共同基金(コミュニティー・チェスト) |
| 4 | バルティック通り |
| 5 | 所得税 |
| 6 | リーディング鉄道 |
| 7 | オリエンタル通り |
| 8 | チャンス |
| 9 | バーモント通り |
| 10 | コネチカット通り |
| 11 | 刑務所、刑務所見学 |
| 12 | セントチャールズプレース |
| 13 | 電力会社 |
| 14 | ステーツ通り |
| 15 | バージニア通り |
| 16 | ペンシルバニア鉄道 |
| 17 | セントジェームスプレース |
| 18 | 共同基金 |
| 19 | テネシー通り |
| 20 | ニューヨーク通り |
| 21 | フリーパーキング |
| 22 | ケンタッキー通り |
| 23 | チャンス |
| 24 | インディアナ通り |
| 25 | イリノイ通り |
| 26 | B&O 鉄道 |
| 27 | アトランティック通り |
| 28 | ベントノール通り |
| 29 | 水道会社 |
| 30 | マービンガーデン |
| 31 | GO TO JAIL(刑務所へ行け) |
| 32 | パシフィック通り |
| 33 | ノースキャロライナ通り |
| 34 | 共同基金 |
| 35 | ペンシルバニア通り |
| 36 | ショートライン鉄道 |
| 37 | チャンス |
| 38 | パークプレース |
| 39 | 物品税 |
| 40 | ボードウォーク |



















コメント