こんにちは、おはようございます、こんばんは、理系夫婦の夫たんたん(@rikeifufu_otto)です!
今日は、2019年の超大型連休GW(10連休!)の3日目。
折角の長期休みなのでちょっと凝ったことでもしようかと、pythonで動画(gif)を作ってみました。
 まほちゃん
まほちゃんそれより、どっか連れってよ!



勉強が先だ!and めんど〜い



ひ、ひどい親だ・・・



・・・
pythonでアニメーションを作るには
今回はpythonで動くグラフ(アニメーション)を作ってみたいと思います。
pythonのグラフ作成モジュール「matplotlib」には、アニメーションを作成するツールが2つ用意されている。
- ArtistAnimation: あらかじめ計算結果を格納しておき、plot時には静止グラフを繋げる
- FuncAnimation: plot時に、その都度計算を行う
今回は計算量が毎回大きそうなので、「ArtistAnimation」で作ってみました。
簡単な例
まずは非常に簡単な例を示したいと思います。
#######
#2019/4/29 TanTan
#Animation easy
#######
import matplotlib.pyplot as plt
import matplotlib.animation as animation
fig = plt.figure() #データをplotするグラフを1つ用意する
plt.xlim(0, 200) #表示するx軸の範囲を設定
plt.ylim(0, 200) #表示するy軸の範囲を設定
plt.xlabel("x axis") #x軸の説明
plt.ylabel("y axis") #y軸の説明
plt.gca().set_aspect('equal', adjustable='box') #グラフ範囲を真四角する
graph_list = [] #各時刻でのグラフを全て格納する場所を用意する
for i in range(100): #100個のグラフを作成して、1つのアニメーションにする
x = i #xの値の変化
y = 2 * i #yの値の変化
graph = plt.scatter(x, y, color="black") #座標(x, y)に点を1つ打ったグラフを作成
graph_list.append([graph]) #上記のグラフをgraph_listへ格納する
ani = animation.ArtistAnimation(fig, graph_list, interval=200) #graph_list内のグラフを連続的に繋げて、200ms毎に表示するアニメーションにする
plt.show() #アニメーションを表示する
ani.save("output_easy.gif", writer="imagemagick") #アニメーションをgifとして保存する
上記の結果が下記のgifです。

このプログラムでの肝の部分は17行目からのfor文のところです。
このループでは、座標(x, y)が毎回更新されます。xはループ文の指標iと同じで、yはiの2倍の値が代入されます。
この座標でplotを20行目で行い、21行目でアニメーションの元になるリストへ格納されます。
作られたリストgrapha_listは最終的に、23行目でアニメーションに加工されて、表示(24行目)やファイル保存(25行目)されます。
(なお最後のgif化する部分は「imagemagick」をインストールしておく必要がある?)
N体シミュレーションの例
上記のアニメーション化の道具を利用して、重力相互作用のみが働く天体運動をシミュレーションしてみようと思いました。
天体が2次元空間に、初期位置と初期速度をもってばらまかれ、時間発展とともに各天体が重力相互作用のためにどのように動くかを計算、アニメーション化するのが目的です。
これが実はなかなか難しかったです。。。
ものすごく簡単な物理モデルを仮定しました。
ある1つの天体が、次の時間ステップの時の位置と速度が次の様に決定されるモデルにしました。
x方向は、
$$ x_{i+1} = x_i + v_{x,i}\Delta t + a_{x,i}\frac{(\Delta t)^2}{2} \\ v_{x,i+1} = v_{x,i} + a_{x,i}\Delta t $$
y方向は、
$$ y_{i+1} = y_i + v_{y,i}\Delta t + a_{y,i}\frac{(\Delta t)^2}{2} \\ v_{y,i+1} = v_{y,i} + a_{y,i}\Delta t $$
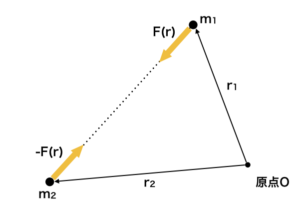
ここで、\( a_{x,i}, a_{y,i} \)は万有引力による他の天体からの合計力によるそれぞれの方向での加速度です。式にすると下記です。(注目している天体を\( \eta \))だとして、
$$ a_{x,i} = \frac{1}{m} \Sigma_{\zeta \neq \eta}G\frac{m\cdot m}{r_\zeta^2} \frac{x_\zeta – x_\eta}{r_\zeta} \\ a_{y,i} = \frac{1}{m} \Sigma_{\zeta \neq \eta}G\frac{m\cdot m}{r_\zeta^2} \frac{y_\zeta – y_\eta}{r_\zeta} $$
ここで\( r_\zeta \)は天体\( \zeta \)と今注目している天体\( \eta \)の距離である。また天体の質量は全て同じ\( m \)とした。
$$ r_\zeta = \sqrt{(x_\zeta – x_\eta)^2 + (y_\zeta – y_\eta)^2} $$
イメージ図:
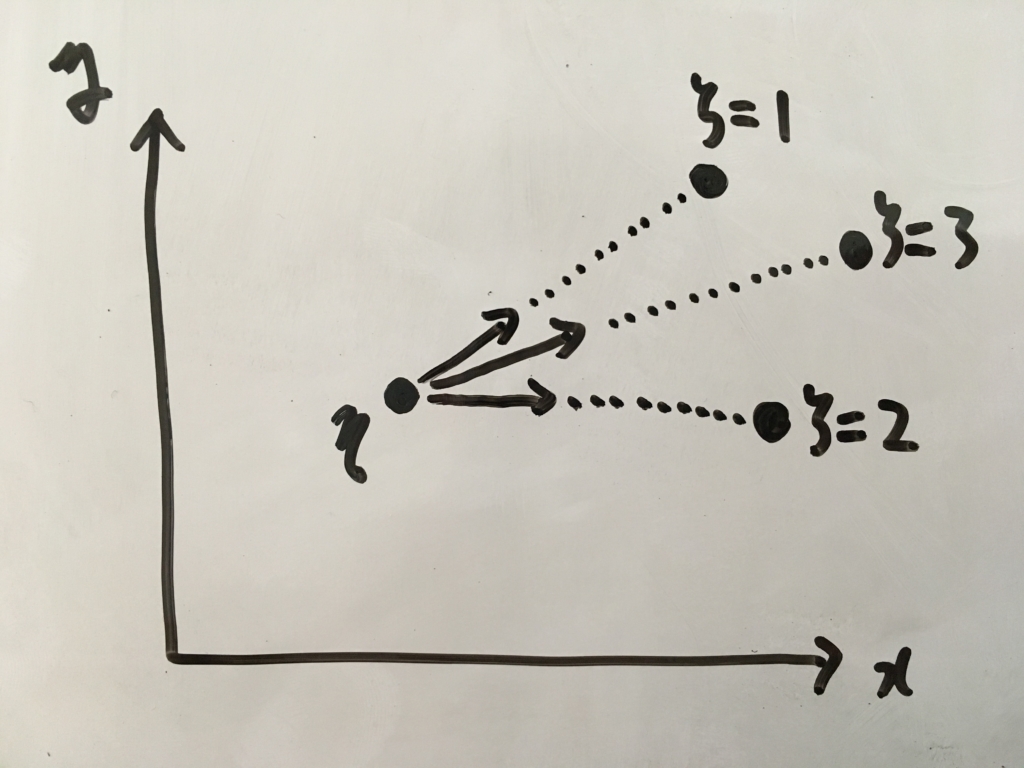

この計算を適当な時間間隔(\( dt \))で全天体に対して行うことで、天体の運動がシミュレーションできるだろうと考えたわけです。
コードが下記。
#######
#2019/4/29 TanTan
#Animation 2D
#######
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import math
import copy
def main():
global mass, G, dt
np.random.seed(seed=3)
#定数
m_earth = 5.9724e24 #地球質量[kg]
T_day = 86400 #1日の秒数[s]
G = 6.674e-11 #[m^3 kg^-1 s^-2] 6.674e-11
#天体数
partN = 2
#天体情報
mass = m_earth * 10.0 #[kg]
#計算分解能時間
dt = T_day * 0.1
#動画
T_all_day = 6000 #計算する全日にち[day]
T_div = 100 #動画用画像数[枚]
#初速度[m/s]
v_0 = 3.0e3
#ステップ計算
T_all = int(T_day * T_all_day / dt)
T_interval = int(T_all/T_div)
#グラフのセットアップ
fig = plt.figure()
plt.xlim(-1e11, 1e11)
plt.ylim(-1e11, 1e11)
plt.xlabel("x [m]")
plt.ylabel("y [m]")
plt.gca().set_aspect('equal', adjustable='box')
#初期値設定
x_0 = []
y_0 = []
vx_0 = []
vy_0 = []
E_k = []
E_p = []
for part in range(partN):
x_0.append(np.random.randint(-2e10, 2e10))
y_0.append(np.random.randint(-2e10, 2e10))
vx_0.append((np.random.rand()*2.0-1.0)*v_0)
vy_0.append((np.random.rand()*2.0-1.0)*v_0)
E_k.append(0)
E_p.append(0)
#2体の天体のみを用意した場合に有効にする。
x_0 = [-0.1e11, 0.1e11]
y_0 = [-0.01e11, 0.01e11]
vx_0 = [0, 0]
vy_0 = [1.0e2, -1.0e2]
#初期値代入
x_c = copy.copy(x_0)
y_c = copy.copy(y_0)
vx_c = copy.copy(vx_0)
vy_c = copy.copy(vy_0)
#アニメーションのデータ作成
ims = []
Energy = []
Energy_Time = []
Energy_k = []
Energy_p = []
Energy_T = []
for time in range(T_all):
cx_s = []
cy_s = []
for i in range(partN):
x_c[i], y_c[i], vx_c[i], vy_c[i], E_k[i], E_p[i] = gravity(x_c, y_c, vx_c, vy_c, i)
sum_K_k = sum(E_k)
sum_K_p = sum(E_p)
total_E = sum_K_k + sum_K_p
Energy_Time.append(time*dt)
Energy_k.append(sum_K_k)
Energy_p.append(sum_K_p)
Energy_T.append(total_E)
if time%T_interval == 0:
im = plt.scatter(x_c, y_c, color="black")
ims.append([im])
Energy.append(Energy_Time)
Energy.append(Energy_k)
Energy.append(Energy_p)
Energy.append(Energy_T)
#アニメーション作成
ani = animation.ArtistAnimation(fig, ims, interval=50)
plt.show(block=False)
ani.save("output.gif", writer="imagemagick")
#エネルギーグラフ作成
Eplot(Energy_Time, Energy_k, Energy_p, Energy_T)
#ユーザーが止めるまで止まらない。
flag = "n"
while flag=="n":
print("Do you want to stop this program? (y/n)")
flag = input('>> ')
def gravity(x_c, y_c, vx_c, vy_c, i):
F_x_sum = 0
F_y_sum = 0
E_p_cont = []
for x_cont, y_cont, j in zip(x_c, y_c, range(len(x_c))):
if i!=j:
r = math.sqrt((x_c[i]-x_cont)**2 + (y_c[i]-y_cont)**2)
F = G*mass*mass/(r*r)
if F > 1.0e200:
print("over!")
F_x = F * (x_cont - x_c[i])/r
F_y = F * (y_cont - y_c[i])/r
F_x_sum = (F_x_sum + F_x)
F_y_sum = (F_y_sum + F_y)
E_p_cont.append(- G * mass**2 / r)
#print(- G * mass**2 / r)
a_x = F_x_sum / mass
a_y = F_y_sum / mass
#速度、位置の計算
vx_c_g = vx_c[i] + a_x * dt
vy_c_g = vy_c[i] + a_y * dt
x_c_g = x_c[i] + vx_c[i]*dt + 0.5*a_x*dt**2
y_c_g = y_c[i] + vy_c[i]*dt + 0.5*a_y*dt**2
#エネルギーの計算
E_k = 0.5 * mass * (vx_c_g**2 + vy_c_g**2)
E_p = sum(E_p_cont)
return x_c_g, y_c_g, vx_c_g, vy_c_g, E_k, E_p
def Eplot(Energy_Time, Energy_k, Energy_p, Energy_T):
fig = plt.figure()
plt.plot(Energy_Time, Energy_k, color="red", label="Kinetic")
plt.plot(Energy_Time, Energy_p, color="green", label="Potential")
plt.plot(Energy_Time, Energy_T, color="black", label="Total")
plt.xlabel("Time [s]")
plt.ylabel("Energy [J]")
plt.legend()
plt.show(block=False)
plt.savefig('figure.png')
return 0
if __name__ == "__main__":
main()
まずは59行目から62行目を有効にして、適当な位置と初速度を持った2天体の場合を計算してみました。結果が下記です。
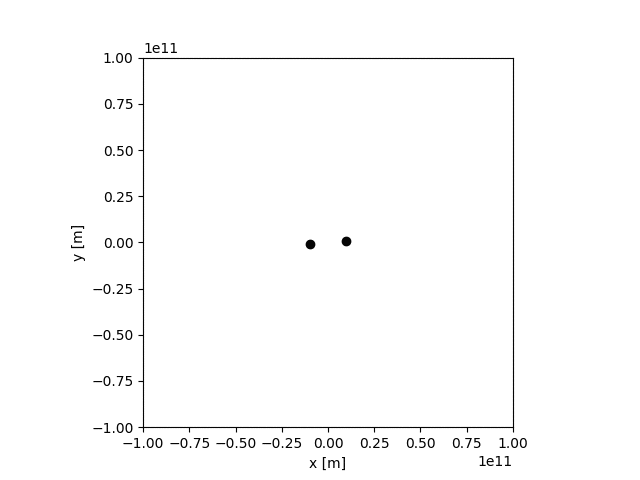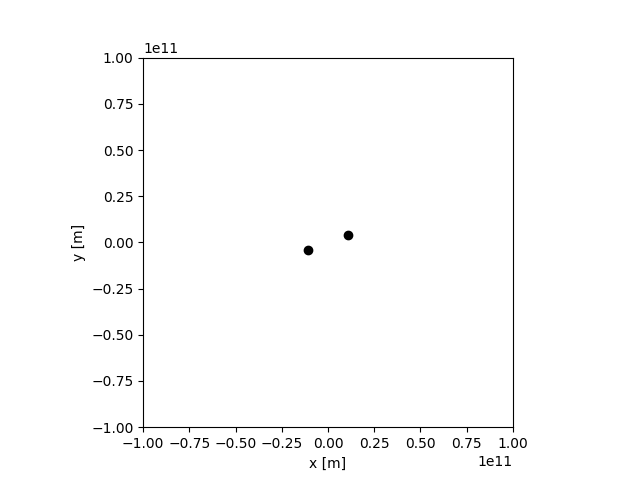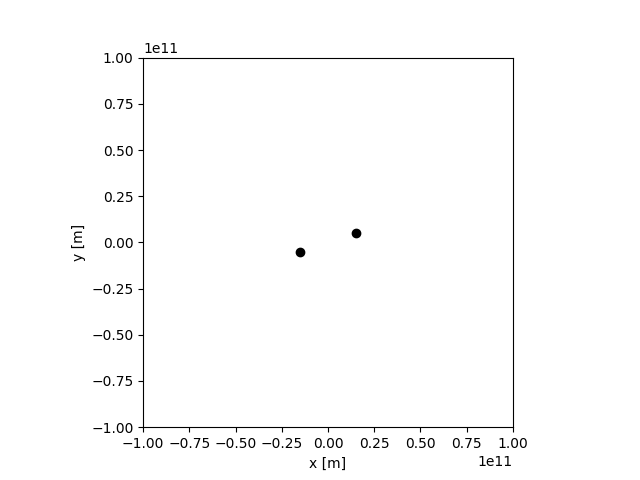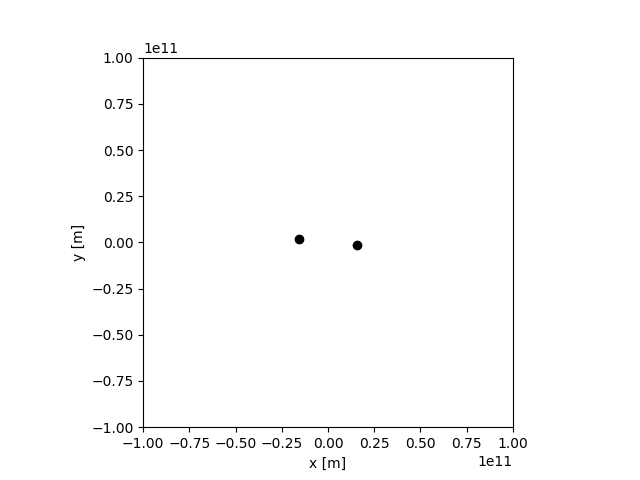

これはそれっぽい結果に見えた。
2つの天体がお互いの周り(実際には2体の重心)を楕円運動している。
3体問題も解いてみました。
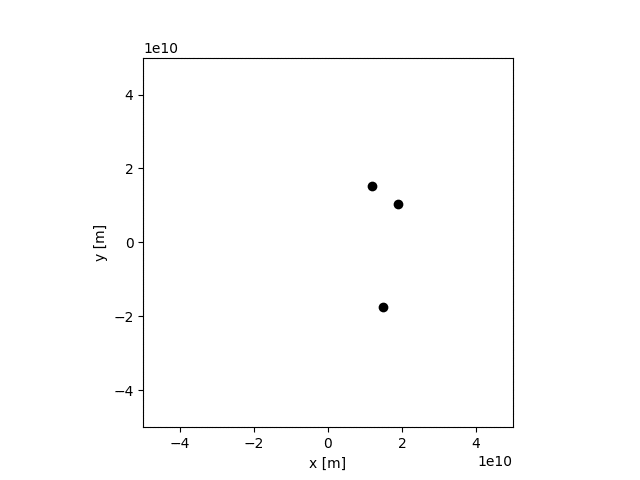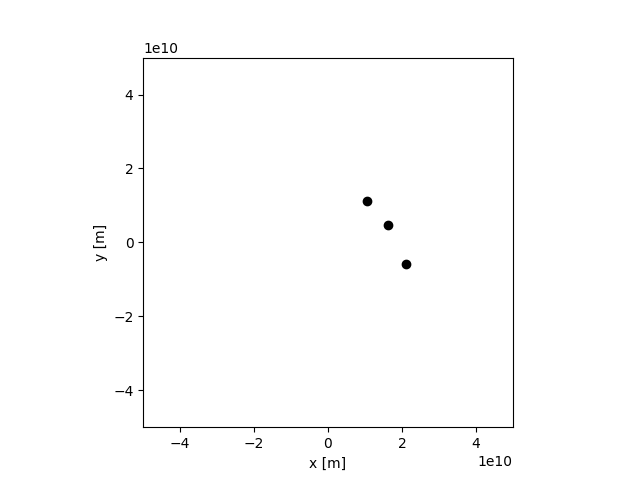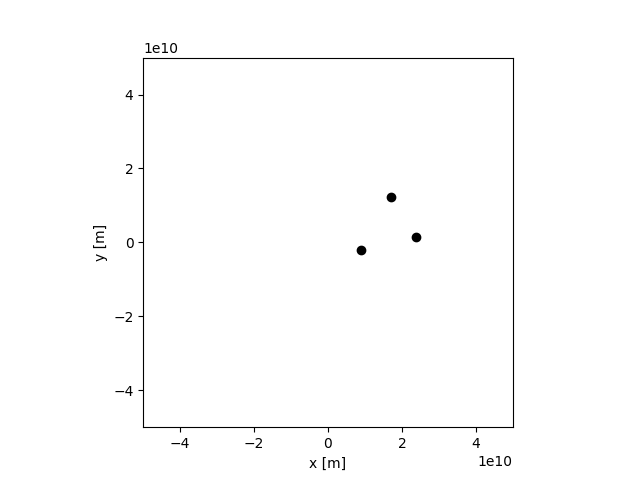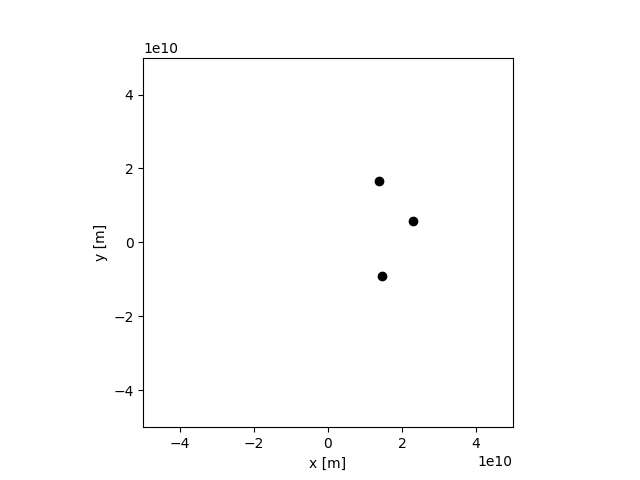

折角なので、天体を100個に設定してみた。
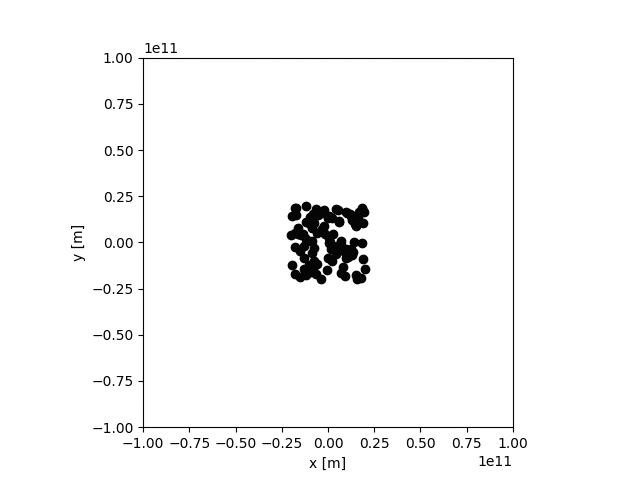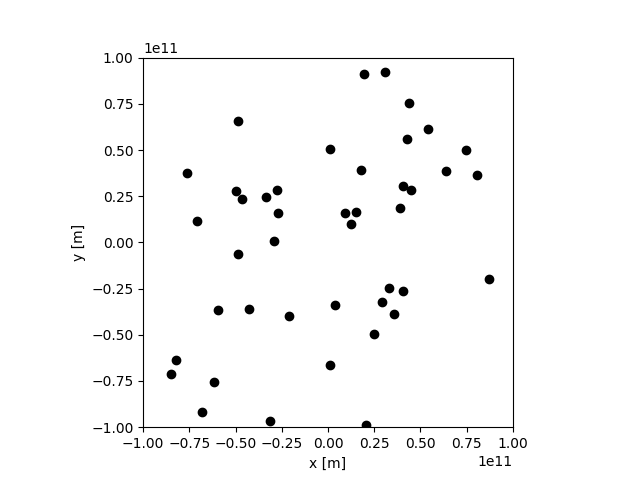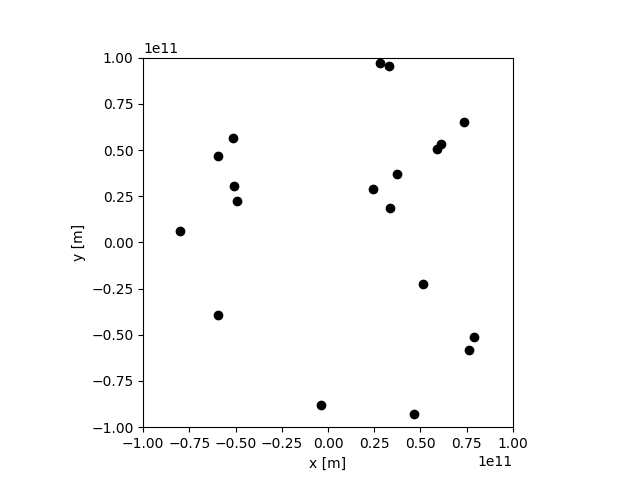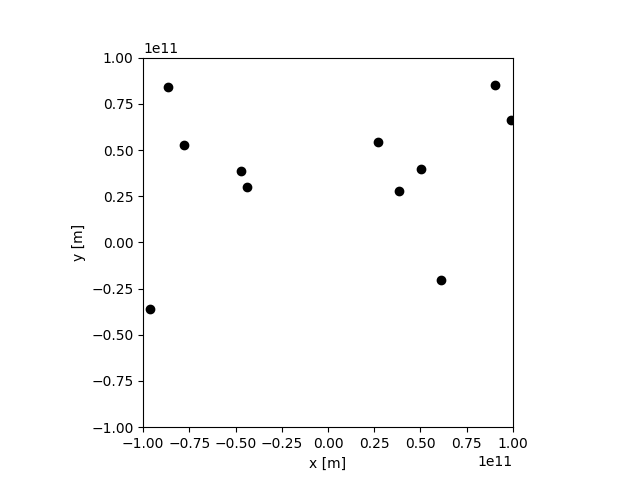

すごい、みんな宇宙の彼方に飛んでいく。
この原因を調べてみるとどうやら、次ステップの計算を行う近似モデルが悪かった様だ。
今回の計算モデルは「リープフロッグ法」と呼ばれる計算手法をもっと簡単にしたので、その時の近似が良くなく、この様なことになったと思います。
もっと計算の時間間隔を細かくすれば多体でもいい感じにできかもしれません。
上記のコード内にはエネルギーの推移を示す部分も含まれるので、みてもらえばわかりますが、エネルギーが増加していきます。
(もしも根本的におかしな点を見つけましたら、ご一報ください。)



中途半端な結果を載せんなよ!



すみません、今回は「アニメーション」作成がメインですので、天体シミュレーションは多めにみてください。
「リープフロッグ法」を真面目に組めばいいのだと思いますが、君のお世話があるので、今日はここまでです!
今度必ず直します!



必ずね!
おススメのプログラミング独学方法はこちらの記事にまとめました!


















コメント