2体問題をイチから解く <数値計算に向けて>

2019年4月30日2019年8月1日

URLをコピーしました！

こんにちは、おはようございます、こんばんは、理系夫婦の夫たんたん(@rikeifufu_otto)です！

前回の記事(GIFアニメーションを作ってみよう★N体シミュレーションを例に添えて★)では、天体の数が増えたり、天体同士が接近しすぎると、計算誤差が大きくなり、エネルギーが保存しなくなってしまいました。

その原因を調べてみると、N体シミュレーションを行う時には、かなりの手法ががある様で、そう簡単にはできない様です。

その手法の1つとして、天体同士が近づいた時に、解析解を代わりに用いるという手法がある様です。

今回はそのための準備として、2体問題の解析解を導いてみようと思う。(2次元)

まほちゃん

今日はGW10連休の4日目なんだけど、どこかに連れて行ってくれないの？？？

たんたん

き、きょうは、ほら、まほちゃんが風邪を引いて、鼻水が止まらないし、天気も悪いし、家の中で勉強した方がいいかなと。。。

まほちゃん

ん〜、じゃ、しょうがないか。明日、治ったらどこかに連れてけよ？

導入と方針

今回は、2つの天体が重力のみの力を及ぼしあって運動する時の動きを計算する「2対問題」を解析的に解きたい、つまり2つの天体の位置を時間の関数として表したいと思います。

この問題は力学の問題でも重要な問題であるので、解説はいろいろ転がっているが、実は、時間変化を記述しているものが少ない。

というのはこの問題から導かれる結果は、「惑星の軌道」だったり、「ケプラーの法則」だったり、「換算質量」だったり、「有効ポテンシャル」だったりとみんながものすごく興味引く点、議論の盛り上がる点があるので、「時間変化の計算」に関してはあまり注目されていないように思う。

私の今回の興味は、そういう定性的な点よりも定量的な「時間変化の計算」に興味があります。なぜなら天体の動きをシミュレーションしたいので。

今回は微小相対変位( $ {\rm d}r, {\rm d}\theta $ )を微小時間( $ {\rm d}t $ )で表せることをゴールとしました。

その先の議論はひとまず他のWebページなどにお任せをしたいと思います。

今回はちょっと方針が複雑なので図示してみました。

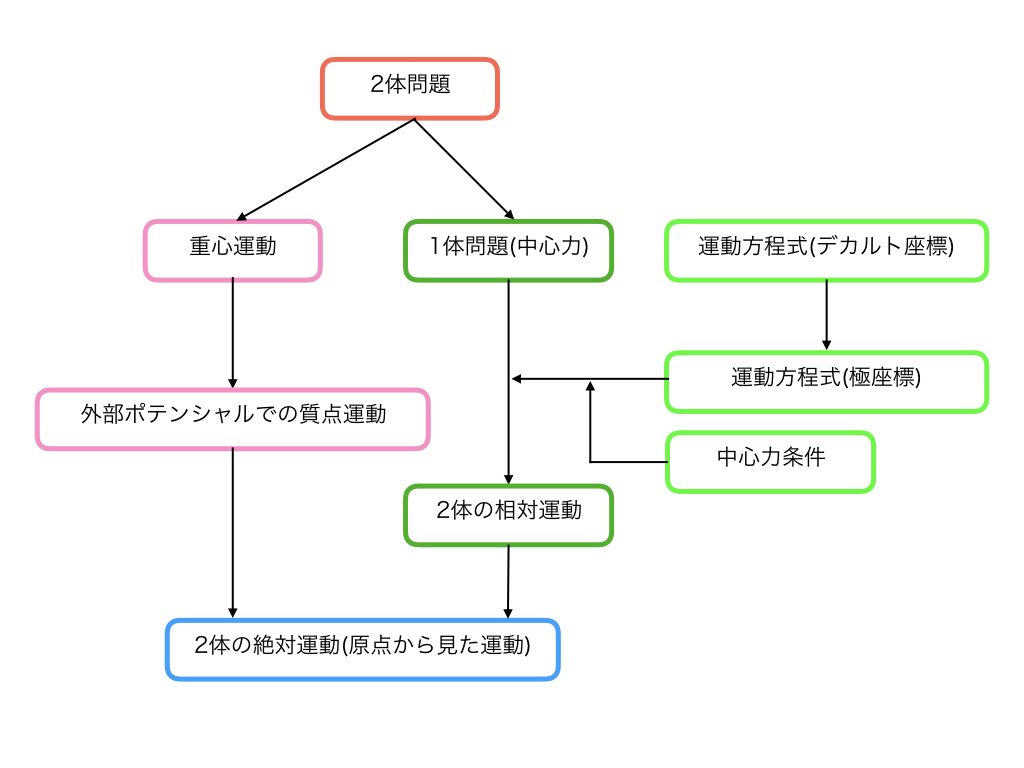
まず2体問題の運動方程式を変形して、重心運動と中心力が働いている1体問題に帰着させます。

次にこの2つの運動を別々に解いていきます。

重心運動は簡単で、周りに何もないければ(今回は2つしか天体がないと仮定しているので、なし)力が加わらない、等速直線運動となります。

一方で「1体問題(中心力)」の方は運動方程式をちゃんと解いてあげる必要があります。

ただし、単なる1体問題なので、そこまで複雑でもないです。

見慣れたデカルト座標の運動方程式を極座標に変形し、そこに中心力という条件を加えて、エネルギー保存則を使うと、重力のような中心力が働いている1体運動の解が求まります。

最後に重心運動と2体の相対運動を合わせてやれば、原点から見た2点の座標が時間の関数で求めることができる様になります。

2体問題の分離

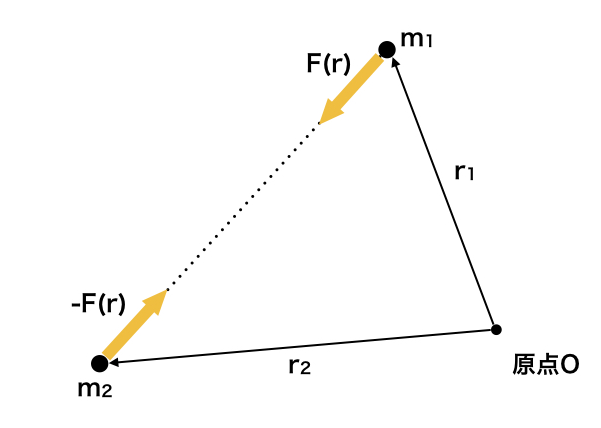
まずは図1から2つの天体に対してそれぞれで運動方程式をとりあえず立ててみる。

$$ m_1 \ddot{{\bf r}}_1 = {\bf F}(r) \ \ \ \ (eq.1) \\ m_2 \ddot{{\bf r}}_2 = -{\bf F}(r) \ \ \ \ (eq.2) $$

どちらも同じ重力($ {\bf F} $)が働いていますが、方向が逆なので、天体2の方には負号をつけました。

またここで$ r $は2天体間の距離を表しています。

$$ r = |{\bf r}| = |{\bf r}_1 – {\bf r}_2| \ \ \ \ (eq.3)$$

上記の2つの運動方程式を変形して、重心運動と1体問題へ帰着させます。

2式(eq.1とeq.2)の両辺をそのまま足すと、

$$ m_1\ddot{{\bf r}}_1 + m_2\ddot{{\bf r}}_2 = 0 $$

となり、重心ベクトル$ {\bf r}_c $は

$$ {\bf r}_c = \frac{m_1{\bf r}_1 + m_2 {\bf r}_2 }{m_1 + m_2} \ \ \ \ (eq.4)$$

とかけるので、重心の運動は、

$$ \ddot{{\bf r}}_c = 0 $$

で特徴付けられる。つまり等加速度運動をすることになる。

今回は2天体以外は天体も力場もないので、重心の慣性の法則にたどり着いたということですね。

次に2式(eq.1とeq.2)をちょっと変形してから、引いてみる。

$$ \ddot{{\bf r}}_1 = \frac{{\bf F}(r)}{m_1} \\ \ddot{{\bf r}}_2 = -\frac{{\bf F}(r)}{m_2} $$

より、

$$ \ddot{{\bf r}}_1 – \ddot{{\bf r}}_2 = \left( \frac{1}{m_1} – \frac{1}{m_2} \right){\bf F}(r) $$

よって、

$$ \ddot{{\bf r}} = \frac{m_2 – m_1}{m_1 m_2}{\bf F}(r) $$

これを書き換えると、

$$ \frac{m_1 m_2}{m_2 – m_1}\ddot{{\bf r}} = {\bf F}(r) $$

ここで、換算質量$ \mu $を次の様に定義する。

$$ \mu \equiv \frac{m_1m_2}{m_2 – m_1} $$

上の運動方程式は、次の様になる。

$$ \mu \ddot{{\bf r}} = {\bf F}(r) \ \ \ \ (eq.5)$$

これは質量$ \mu $を持つ質点の中心力における運動方程式そのものになる。

この様にして2体問題は重心運動と1体問題(中心力)に分離できた。

ここで$ {\bf r}_1, {\bf r}_2 $を$ {\bf r}_c, {\bf r} $で表してみる。

eq.3, eq.4によって、下記になることがわかる。

$$ {\bf r}_1 = {\bf r}_c + \frac{m_2}{m_1 + m_2}{\bf r} \ \ \ \ (eq.6) \\ {\bf r}_2 = {\bf r}_c + \frac{m_1}{m_1 + m_2}{\bf r} \ \ \ \ (eq.7) $$

この2式が表していることは、何らかの方法(例えば下記で説明する方法)で$ {\bf r}_c, {\bf r} $が求まれば、$ {\bf r}_1, {\bf r}_2 $が求まり、2つの天体の軌跡(軌道)が描けるということになる。

$ {\bf r}_c $はすでに上記で等速直線運動をするということがわかっているのであとは$ {\bf r} $がわかれば良い。つまりeq.5が解ければ良い。

デカルト座標での運動方程式 → 極座標での運動方程式

上記までで、あとは中心力が働いている運動方程式を解けば良いことがわかる。

中心力なので、デカルト座標よりも極座標の方が何かと便利なので、デカルト座標の運動方程式を極座標で表してみたい。

ひとまず働いている力は任意の力を考える。

系を図示しておく。

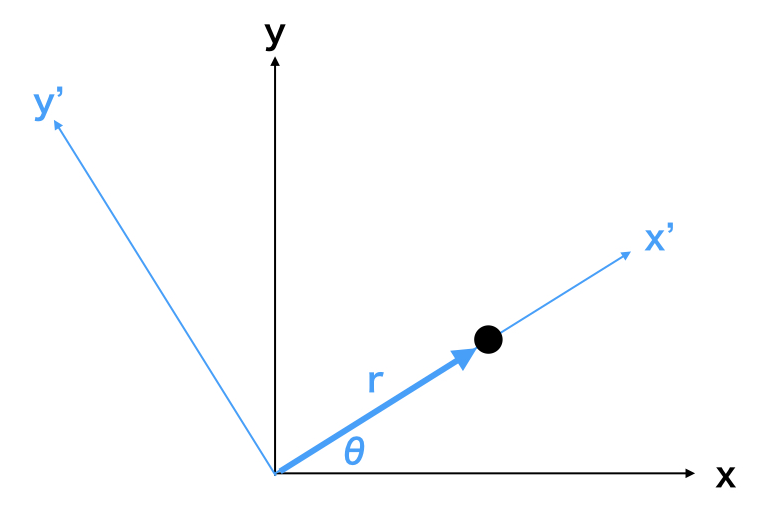
まずは、極座標表記へ変換して、次に($ x, y $) → ( $ x’, y’ $ )という座標変換を考えて、加速度を求めてみる。

$$ x = r\cos \theta \\ y = r \sin \theta $$
これを時間で1階微分してみる。

$$ \dot{x} = \dot{r}\cos\theta – r\sin\theta \dot{\theta} \\ \dot{y} = \dot{r}\sin\theta + r\cos \theta \dot{\theta} $$

さらにもう一階微分して、加速度にする。こうすることで運動方程式まで結び付けられる。

$$ \ddot{x} = \ddot{r}\cos\theta – 2\dot{r}\sin \theta \dot{\theta} – r\cos\theta\dot{\theta}^2 – r\sin \theta\ddot{\theta} \ \ \ \ (eq.8) \\ \ddot{y} = \ddot{r}\sin\theta + 2\dot{r}\cos\theta\dot{\theta} – r\sin\theta\dot{\theta}^2 + r\cos\theta\ddot{\theta} \ \ \ \ (eq.9)$$

また座標変換から

$$ \left( \begin{array}{c} \ddot{x’} \\ \ddot{y’} \end{array} \right) = \left( \begin{array}{c c} \cos\theta & \sin\theta \\ -\sin\theta & \cos \theta \end{array} \right) \left( \begin{array}{c} \ddot{x} \\ \ddot{y} \end{array} \right) $$

であるので、これにeq.8, eq.9を代入すると、

$$ \ddot{x’} = \ddot{r} – r\dot{\theta}^2 \\ \ddot{y’} = 2\dot{r}\dot{\theta} + r\dot{\theta}^2 = \frac{1}{r}\frac{{\rm d}}{{\rm d}t} (r^2\dot{\theta}) $$

今任意の力を考えているので、力を$ r $方向($ F_r $)とそれに直行する方向($ F_\theta $)とに分けると次のような運動方程式が成り立つ。ここで質量には$ \mu $を使用する。

$$ \mu\ddot{x’} = \mu(\ddot{r} – r\dot{\theta}^2) = F_r \ \ \ \ (eq.10) \\ \mu\ddot{y’} = \mu\left( \frac{1}{r}\frac{{\rm d}}{{\rm d}t} (r^2\dot{\theta}) \right) = F_\theta \ \ \ \ (eq.11)$$

中心力条件

eq.10, eq.11に中心力という条件を付加する。

$$ \ddot{x’} = \frac{f(r)}{\mu} = \ddot{r} – r\dot{\theta}^2 \ \ \ \ (eq.12) \\ \ddot{y’} = 0 = \frac{1}{r}\frac{{\rm d}}{{\rm d}t} (r^2\dot{\theta}) \ \ \ \ (eq.13) $$

注目すべきeq.13について考えてみる。時間微分が0ということは、

$$ r^2\dot{\theta} = 一定 \equiv A \ \ \ \ (eq.14)$$
となる。

ここから

$$ \dot{\theta} = \frac{A}{r^2} \ \ \ \ (eq.15)$$

となることがわかる。

ちなみにeq.14はケプラーの法則の1つである面積速度一定の法則を意味している。

eq.12については実は今回の目的を達成するためには特に必要ない。

あとはエネルギー保存則を利用して、どうにかするからである。

エネルギー保存則から運動を導く

上記のeq.15まで導けたら、今度はエネルギー保存則を用いれば、この中心力(重力)が働いている1体問題が解ける。

運動エネルギー$ K $、ポテンシャルエネルギー$ V $をそれぞれ求める。

$$ K = \frac{\mu}{2}(\dot{x}^2 + \dot{y}^2) \\ = \frac{\mu}{2}( \dot{r}^2\cos^2\theta – 2r\dot{r}\cos\theta\sin\theta\dot{\theta} + r^2\dot{\theta}^2\sin^2\theta + \dot{r}^2\sin^2\theta + 2r\dot{r}\cos\theta\sin\theta\dot{\theta} + r^2\cos^2\theta\dot{\theta}^2 ) \\ =\frac{\mu}{2}( \dot{r}^2 + r^2\dot{\theta}^2 ) \\ = \frac{\mu}{2}\left( \dot{r}^2 + \frac{A^2}{r^2} \right) \ \ \ \ (eq.16)$$

ここでは先のeq.15を使用した。

$$ V = V(r) \ \ \ \ (eq.17)$$

eq.16, eq.17を用いて全エネルギー$ E $を求めると、

$$ E = K + V = \frac{\mu}{2}\left( \dot{r}^2 + \frac{A^2}{r^2} \right) + V(r) \ \ \ \ (eq.18)$$

となる。エネルギーが保存することからこれは初期エネルギー$ E_0 $にイコールである。

よってeq.18は次の様に変形できる。

$$ \dot{r}^2 = \frac{2}{\mu}\left( E_0-\frac{\mu}{2}\frac{A^2}{r^2} – V(r) \right) $$

$$ \frac{{\rm d}r}{{\rm d}t} = \pm\sqrt{\frac{2}{\mu}}\sqrt{E_0-\left( V(r)+\frac{\mu}{2}\frac{A^2}{r^2} \right)} $$

$$ {\rm d}r = \pm \sqrt{\frac{2}{\mu}}\sqrt{E_0-\left( V(r)+\frac{\mu}{2}\frac{A^2}{r^2} \right)} {\rm d}t $$

この様にして、$ {\rm d}r $を$ {\rm d}t $で表すことができました。

あとは$ V(r) $に重力ポテンシャルを代入してあれば良い。

$$ {\rm d}r = \pm \sqrt{\frac{2}{\mu}}\sqrt{E_0+\left( G\frac{m_1m_2}{r}-\frac{\mu}{2}\frac{A^2}{r^2} \right)} {\rm d}t \ \ \ \ (eq.19)$$