公園でハナタカ！ブランコを物理的に分析してみた

2019年4月14日2019年12月16日

URLをコピーしました！

こんにちは、おはようございます、こんばんは、理系夫婦の夫たんたん(@rikeifufu_otto)です！

今回はブランコについて考えを深めて、子供に自慢できる知識をちょっとだけお教えいたします！

皆さん、想像してみてください。

自分が子供や他の人に、物理の言葉でブランコの現象を説明していることを。

子供や異性の「すごい！パパ、かしこ〜い！」「OOさんったら、あったまいい〜！」という声が脳裏に浮かびますか？

それとも「嫌！きもい！」でしょうか。。。

背景

この間、まほちゃんとブランコで遊んでいた時のことです。

二人で隣り合ったブランコに乗って、それぞれでゆらゆらして遊んでいました。

「同じ形(長さ)のブランコに乗っていると、体重の重いパパでも、体重の軽いまほちゃんでも、同じ周期で揺れるんだよ。」

と、私は2歳児に向かって説明をしました。

しかし！その時、なんと、まほちゃんのブランコと私の乗ったブランコでは明らかに周期が違っていたのです！

物理をあまりかじっていない方だと、この驚きに疑問を感じるかもしれません。

物理を習いたての方なら、この驚きに共感いただけるでしょう。

また、物理に自信がおありの方だと、瞬時に周期の違いの原因がわかるでしょう。とともに私(パパ)とまほちゃん(2歳児)のどっちが、周期の方の短い方か想像つくかと思います。

今回は、まずできる限り誰でも理解しやすいようにこの疑問を解説して、さらに答えもお教えいたします。

次にちゃんと運動方程式を立てて、その微分方程式を一歩一歩解いていきます。

なぜ、周期が違うことに驚いたか

ブランコというのは、単純化してみると、振り子になるんです。

昔の柱時計とかには、振り子が付いていますよね？あれと同じです。

柱時計の振り子は、単なる飾りではなく、実はこの揺れによって1秒を決めています。

物理ではこれを「単振り子」と呼んでいます。

この単振り子には面白い性質があるのです。

振り子が、ある位置(例えば一番右の位置)から動いてまた同じ位置(速度の方向も含めて同じ)に戻るまでの時間(=周期)$ T $は振り子の長さ$ l $と地球の重力の強さにのみ依存します。式で表すと下記になります。

$$ T = 2\pi\sqrt{\frac{l}{g}} $$

ここで$ g $は9.8$ {\rm m/s^2} $で重力加速度と呼ばれる定数です。

振り子の糸の長さが長ければ、その分周期が長くなります。

公園にある様なブランコと、ハイジのブランコくらい大きなブランコを想像すると、ハイジのブランコの方が1周期が長いことが想像できるかと思います。

ちなみに公園のブランコ(長さが2mと仮定)の場合だと、周期は次の様になります。

$$ T = 2\pi\sqrt{\frac{2}{9.8}} = 2.8 [{\rm s}] $$

3秒ほどで揺れていることは感覚とも一致するかと思います。

さらに最初の式から分かることは、周期はぶら下がっている物体の重さに寄らないのです。

そう、重い物体(パパ)がブランコに乗ろうと、軽い物体(2歳児)がブランコに乗ろうと、周期は一致するはずです。

これは物理界では常識だったので、驚いたわけです。

なぜ、周期が違ったのか

ここでなぜ周期が違ったのでしょうか。

数式はちゃんと正しいです。

正しくなかったのは、頭の中の「近似」でした。

振り子の長さ$ l $はブランコの長さとして近似するのではなく、ブランコの紐がぶら下がっている支点から乗っている物体の重心までの距離として近似するべきなのです。

人の重心は大体おへその位置だと思いますが、大人と2歳児を比べると体の大きさの分だけ違ってきます。

大人がブランコに座っていた方が、支点から距離が短くなります。

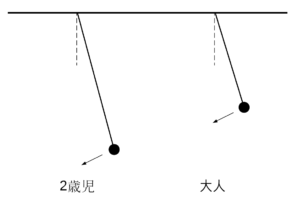
このために$ l $の違いが生じて、周期も違ってきたわけです。

ということで、物理的に考えると、大人と2歳児が乗っているブランコを比べると、大人の体の大きさの分だけ重心が上に移動したことで周期が短くなる、ということです。

ちなみにブランコはネットで買えます。

運動方程式の導出から微分方程式を解くまで

ここまでは中学での知識で十分に理解できるものだったかと思いますが、ここからグッと物理、数学を使っていきます。

今回のテーマ「単振り子」は基本的でかつ重要な物理モデルです。

このモデルの運動方程式を立てて、その上で、その微分方程式を解いて最終的には周期を求めたいと思います。

まず運動方程式から。

力の加わり方を含めた図を下記に書きました。

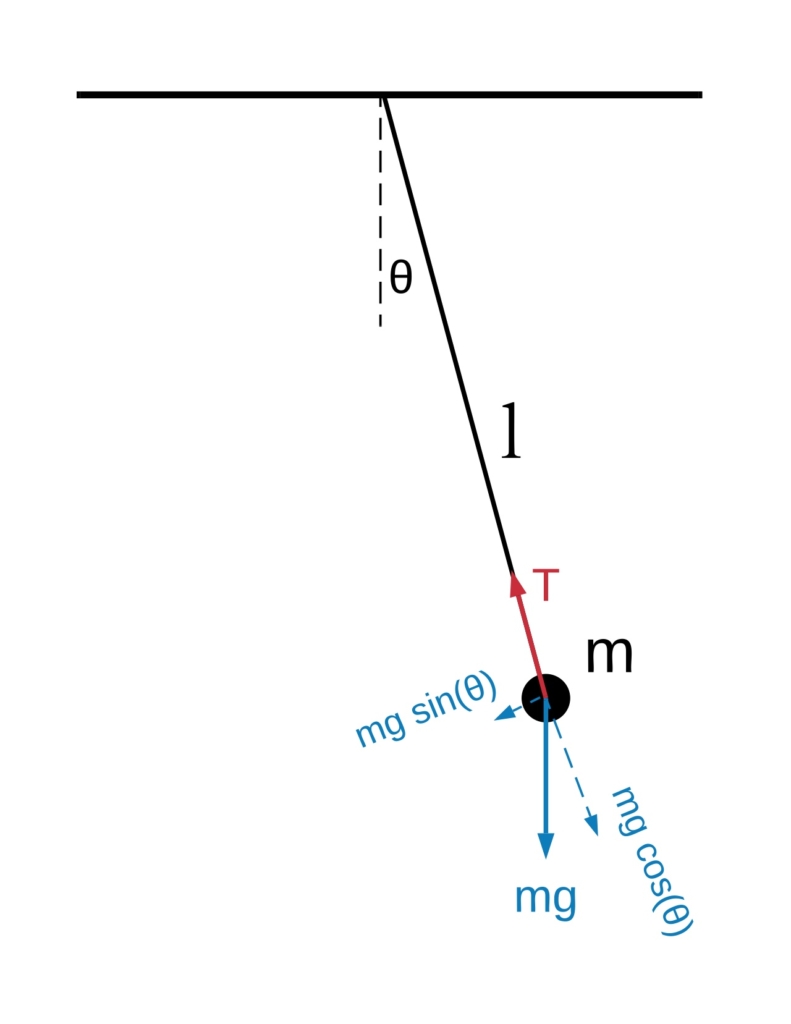
この図では、新たに力を書き加えました。

赤い実線が糸の張力で、青い実線が重力を表しています。

この振り子の動きを想像すると、糸の方向（つまり張力の方向）には動かないとわかるので、その方向ベクトルが物理的に意味のある方向だと勘づけます。

そこで、重力$ mg $もその「張力方向」と「張力に垂直な方向」に分解してみたのが、青い点線の力です。

張力方向は動きがないので、

$$ T = mg\cos \theta $$

である。この式は重要ではないです。

それよりももう一つの方向の力が大事です。

この「張力とは垂直にある方向」の動きが振り子の動きになります。この方向を円弧方向もしくは$ \theta $方向と呼ぶことにします。

$\theta $を使って円弧方向の位置（基準は最低地点）を表すと、$ l\theta $となります。

これの2階時間微分が加速度になります。

以上から、円弧方向の加速度とその方向の力をが表せるので、以下のように運動方程式が立てられます。

$$ ml\frac{{\rm d}^2\theta}{{\rm d}t^2} = mg\sin \theta $$

この微分方程式には$ \sin \theta $ といういかにも非線形で難しい項が入っています。

そこで、$ \theta $が小さいと仮定、つまり揺れが小さいと仮定して、簡単な式にします。

すると運動方程式は次のように簡単になります。（ここの部分がわからない時は「テーラー展開」ってgoogle先生に聞いてみてください。闇にハマります。）

$$ ml\frac{{\rm d}^2\theta}{{\rm d}t^2} = mg\theta \\
\Rightarrow \frac{{\rm d}^2\theta}{{\rm d}t^2} = \frac{g}{l}\theta \ \ \ (eq.1)$$

これが、これから解くべき微分方程式になります。

ここからはもう安心、超簡単です。

と言いたいが、天下り的なのが降ってくるので、簡単に理解は難しい。

eq.1の解になりそうな関数系をまず思いつかないといけない。

微分を2回すると、自分に戻る関数系なので、万能関数$ e^{t} $的な関数系が思いつく。

ということで、少々天下りだが、次の様にeq.1の$ \theta $の解の形を仮定する。

$$ \theta (t) = e^{\lambda t} $$

$ \lambda $に何が入ると、eq.1が成り立つのだろうか。

考える前に行動！ということで、とりあえず代入してみればよい。

$$ \lambda^2 e^{\lambda t} = \frac{g}{l}e^{\lambda t} \\
\Rightarrow \lambda = \pm \sqrt{\frac{g}{l}} $$

この結果から少なくとも次の2つは、それぞれeq.1の解であることが分かる。

$$ \theta (t) = e^{\omega t}, \ \ \ (eq.2) \\
\theta (t) = e^{-\omega t} \ \ \ (eq.3) $$

ただし、

$$ \omega \equiv \sqrt{\frac{g}{l}} $$

とした。

eq.2, 3ともに解であるので、その線型結合も今考えている微分方程式の解であるはずである。というかその方が一般的な表現となる。

$$ \theta (t) = C_1e^{\omega t} + C_2e^{-\omega t} \ \ \ (eq.4)$$

これがeq.1の一般解となる。ただし$ C_1, C_2 $は初期条件などで決まるパラメータである。

しかし、これじゃ物理的な意味がわかりにくいので、もう少し変形していく。

$ C_1, C_2 $を次の様に実部と虚部で表してみることにする。(この作業によって$ C_1, C_2$に何かの制限か加わることはないことはすぐに分かる。)

$$ C_1 = \alpha_1 + i \beta_1 \\
C_2 = \alpha_2 + i \beta_2 $$

eq.4を少し変形してからこれを代入してみる。

オイラーの公式($ e^{\pm i x} = \cos x \pm i \sin x $ )を使用すると、

$$ \theta (t) = C_1e^{\omega t} + C_2e^{-\omega t} \\
= C_1(\cos \omega t + i \sin \omega t ) + C_2(\cos \omega t – i \sin \omega t)) \\
= (C_1 + C_2)\cos \omega t + i(C_1 – C_2)\sin \omega t
$$

と変形できる。

次に$ C_1, C_2 $を代入する。

$$ \theta (t) = \left[ \alpha_1 + \alpha_2 + i(\beta_1 + \beta_2)\right]\cos \omega t + i\left[ \alpha_1 – \alpha_2 + i(\beta_1 – \beta_2)\right]\sin \omega t \\
= (\alpha_1 + \alpha_2)\cos \omega t – (\beta_1 – \beta_2)\sin \omega t + i\left[ (\beta_1 + \beta_2)\cos \omega t +(\alpha_1 – \alpha_2)\sin \omega t \right]
$$

かなり複雑になってしまったが、ここで物理的な「要請」を与える。

それは、「解の中に虚数は出てこない」というものである。
その理由は$ \theta(t) $は角度$ \theta $の時間変化を表しており、実世界の観測できる物理量であるため、虚数が入ってはならないのである。

「角度を測ってみたら、虚数だった」なんてことはあり得ない。

ということで、先の式は次の様になる。

$$ \theta (t) = (\alpha_1 + \alpha_2)\cos \omega t – (\beta_1 – \beta_2)\sin \omega t \ \ \ (eq.5)$$

もう少し変形を頑張ると物理的な性質が見えてくる。

三角関数の合成の公式:

$$ a\sin x + b\cos x = \sqrt{a^2+b^2}\sin (\theta + \delta) \\
\delta = \sin^{-1}\left(\frac{b}{\sqrt{a^2+b^2}}\right)$$

を使用する。

するとeq.5は次の様に変形できる。

$$ \theta (t) = A \sin \left( \omega t + \delta \right) \ \ \ (eq.6)$$

ただし、$ A, \delta $は初期条件で決まる定数である。