まほちゃん電子回路のノイズをみるために、電気信号のファストフーリエ変換(FFT)を行いたいんだけど、いい感じのソフトがないよ😂
それに他の計算とも統一的に扱いたいから、メインで使っている言語のpythonでやりたいけどどうしたらいいの？
たんたんFFTは3歳児にはちょっと早い気もするけど、実装法を解説するね。
まほちゃん46
たんたんFFTは時系列データを周波数空間に写して、その信号にどのような周波数の波が含まれているかをみるための方法だね。
pythonのnumpyを使えば、np.fft.fft(時系列データ)とすればすぐにFFTされたデータが得られるけど、実際にこの機能を現場で使うには周波数軸の計算やノイズ低減のためのオーバーラップ処理、窓関数による事前処理が必要だよ。
FFTとは
FFTとはFast Fourier Transformの略で、日本語では高速フーリエ変換と呼ばれています。
時系列データを、周波数空間に写して、データの周期性を調べることができます。
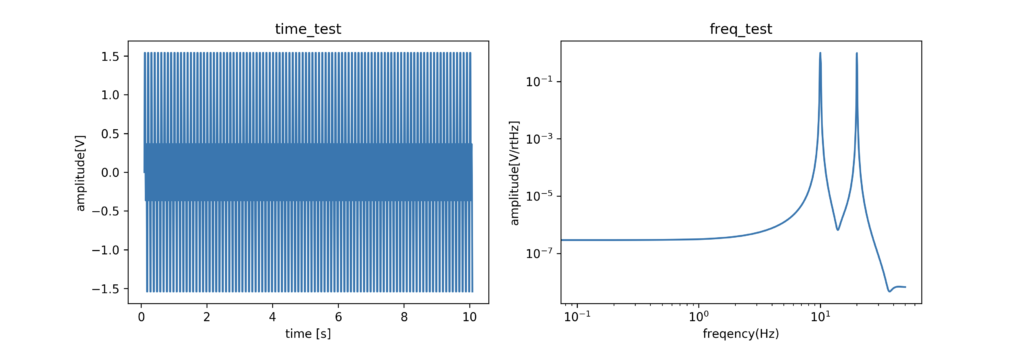
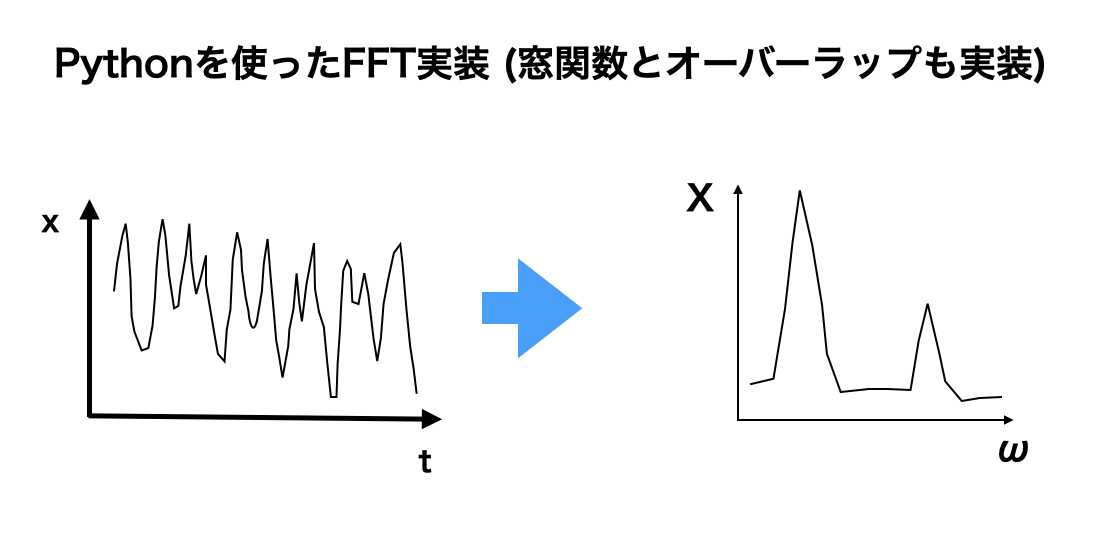
例えば下記のグラフではグジャっとなっている時系列データ(左)を、FFTしてあげると右図のように周波数10Hzと20Hzの波が重なっているデータだということがわかります。
コンピュータで処理を行う場合には実際には「離散フーリエ変換」を行っているが、まぁ細かいことは気にせず。
フーリエ変換の数式
pythonでこのFFTを実装する時には気にする必要は無いんですが、一応フーリエ変換の数式を示しておきます。
時系列データ\( x(t) \)をフーリエ変換して\( X(\omega) \)を得たいとします。
その時に変換式が次です。
$$ X(\omega) = \int_{-\infty}^\infty x(t)e^{-i\omega t} {\rm d}t $$
ここで、\( i \) が虚数単位です。
ちなみに逆フーリエ変換(IFFT)が次式で、周波数空間にある\( X(\omega) \) を時系列データ\( x(t) \) に逆変換できます。
$$ x(t) = \frac{a}{2\pi}\int_{-\infty}^\infty X(\omega)e^{i\omega t} {\rm d}\omega $$
この2つ変換は実際の世の中にはかなり重要で、例えば電気信号の高周波ノイズをカットしたい場合には、FFTして周波数空間に写した後に、高周波成分を削除して、再びIFFTで時系列信号に戻したりする。
PythonでFFTを行う手順
今回は入力信号データはすでに用意されているとします。
このデータは、ある定められたサンプリング周波数( \( \Delta f \) )で測定されているとします。
つまり信号データは\( {\rm d}t = \frac{1}{\Delta f} \) の間隔で並べられているとします。
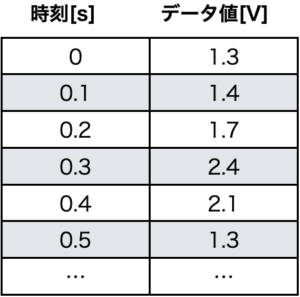
上記の例では、サンプリング周波数は10Hzで時間間隔dtが0.1sです。
FFTを行う手順としては、次の図のようになります。
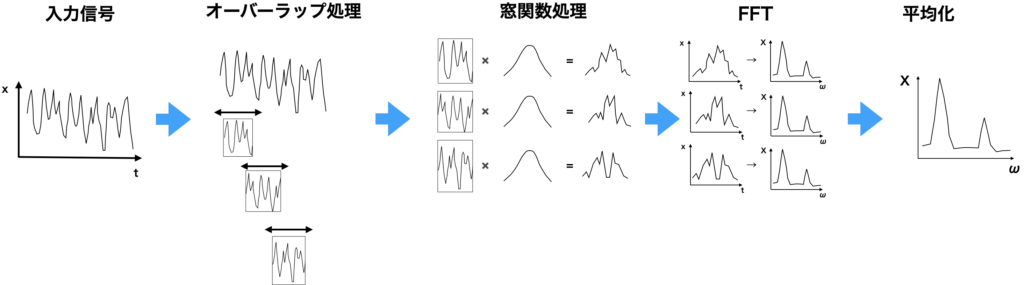
オーバーラップ処理
入力された信号をオーバーラップさせながら分割します。
こうすることでデータの長時間の連続性を犠牲にして、ノイズを低減することができます。
オーバーラップをさせて同じデータ区間を多数回使ってもいいのか？という疑問が出ますが、「良い」です。
完全に同じデータ出なければ、誤差の情報は完全には一致せず、平均化を行うことで、誤差低減が可能です。
単に全時間データを等分割するよりも、1つ1つのデータセット(これは時間フレームと呼ばれる)が長時間の連続データとなりますので、より低い周波数情報を含めることができます。
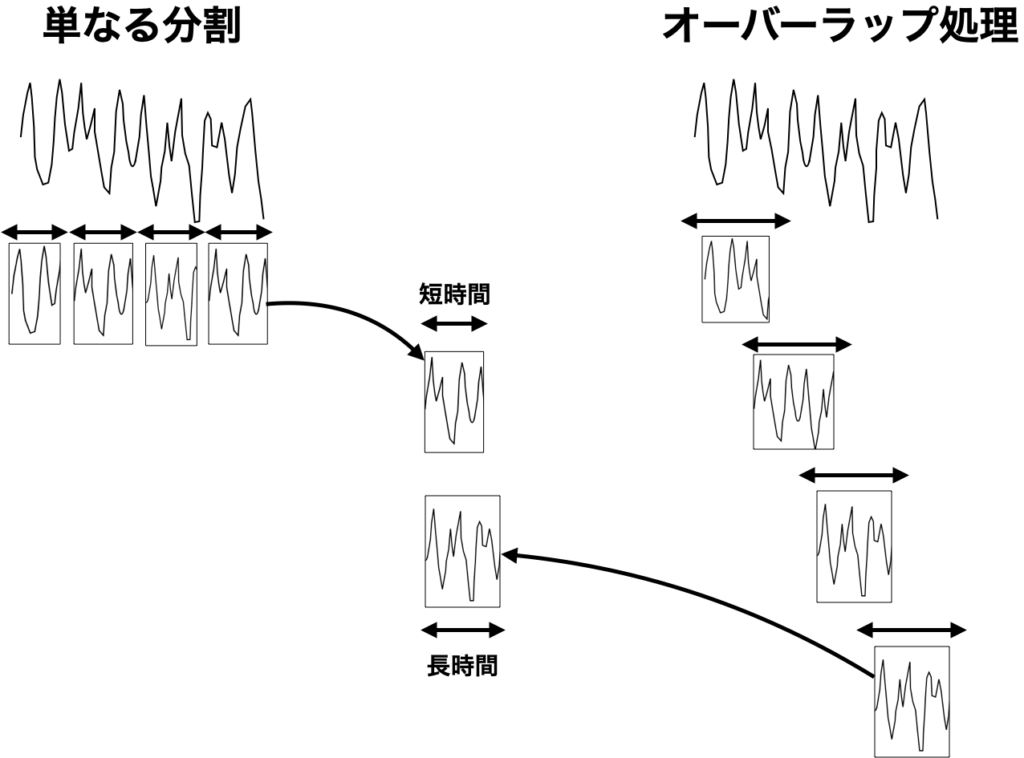
上図のように、単なる4分割よりも、オーバーラップさせた分割の方が1つの時間フレームが「長時間」になります。
長時間データのフーリエ変換を行えば、それだけ低周波の情報が得られることになります。例えば10sの時間データなら0.1Hzの情報が得られるが、100sの長時間なら0.01Hzの情報が得られます。(実際にはナイキスト周波数の情報しか得られないので、0.2Hzと0.02Hzですが、ここでは細かいことは忘れて。)
オーバーラップ処理ではデータを分割したので、各々の時間フレームをFFTした後には、それらを平均化すれば良い。
窓関数処理
FFTにかける前に窓巻数を信号に対して掛けてあげる必要があります。
FFTを行う時の前提条件に、「信号が無限に周期的である」という条件があるからです。
FFTの内部で何が行われているかというと、入力した信号を複製してつなぎ合わせます。
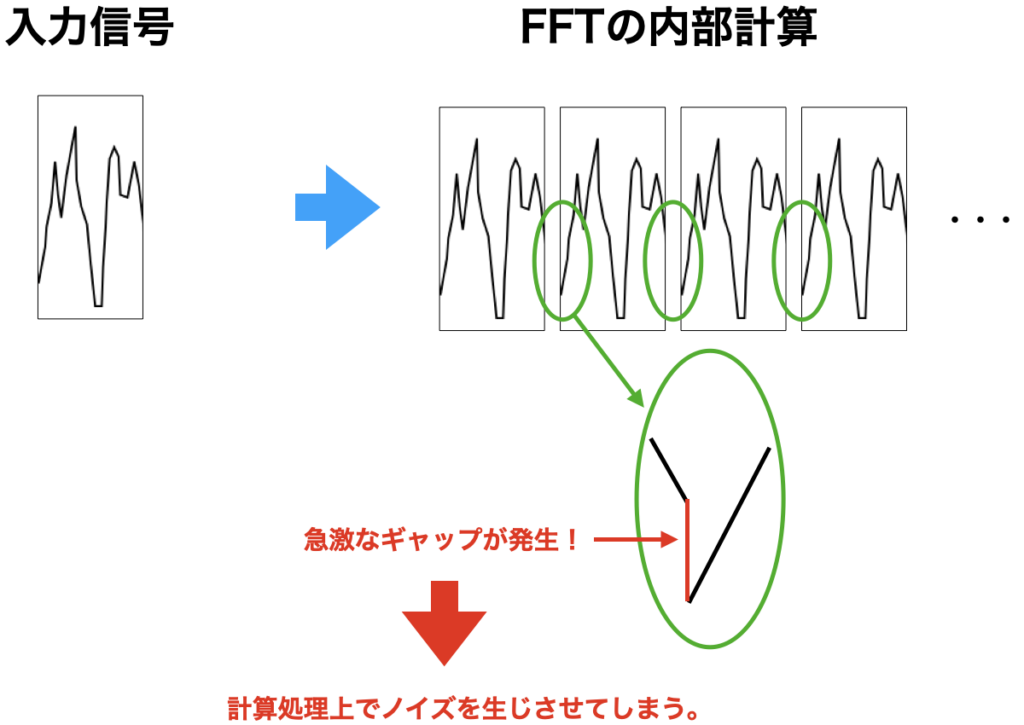
この時に、上図のように、入力信号の最後の値と最初の値は普通同じでないので、つなぎ合わせた場合には急激なギャップが生じてしまいます。
「ギャップ」はいわばステップ関数なので、この部分のフーリエ変換は全周波数領域で多くのノイズを生んでしまいます。(特に低周波で)
なので、コピーした時間フレームの間をいい感じにつなぎ合わせる必要があります。
窓関数を信号に掛ける理由がここにあります。
窓関数はいろいろな種類がありますが、概ね最初と最後は0です。つまり時間フレームを最初と最後を0にしてあげることで緩やかに連続的につなげることができるのです。
下記に3つの窓関数を示しておきます。
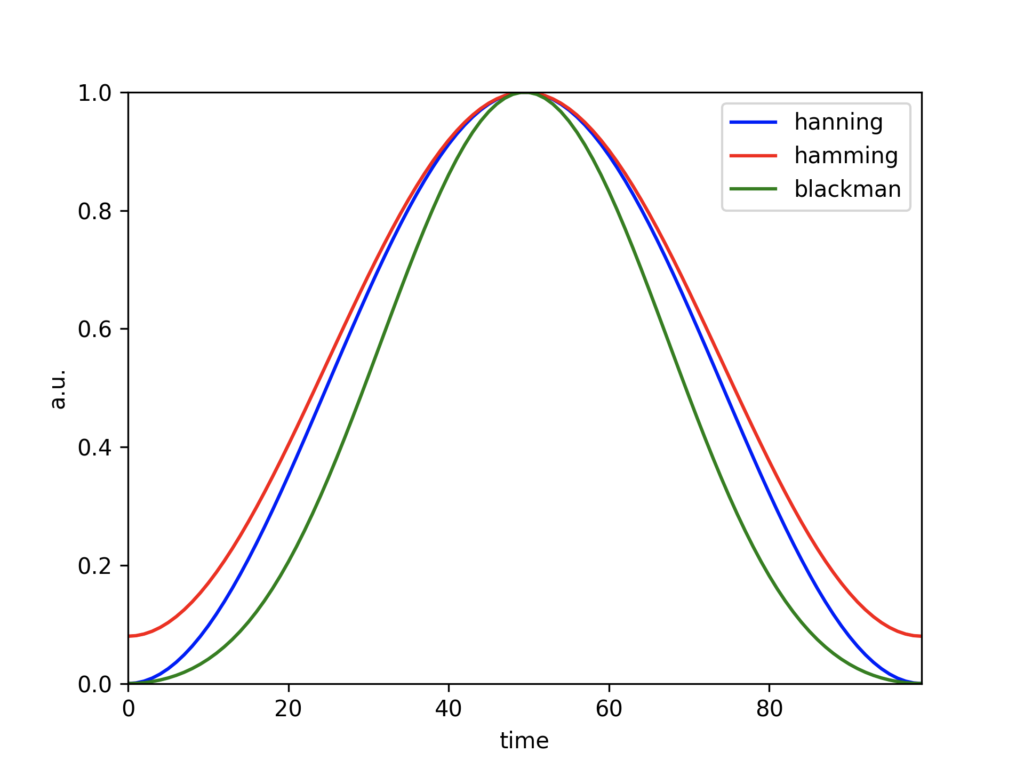
この窓関数の横軸は分割された時間フレームのデータの順番数になります。
例えば1つの時間フレームが10sで0.1Hzのサンプリング周波数なら、窓関数の横軸は0から\( 10\times\frac{1}{0.1}=100 \) となります。
pythonのnumpyを使えば窓関数の生成も簡単です。
|
1 2 3 4 5 6 7 8 9 |
#window fuction生成 import numpy as np N=100 #入力データの数=横軸のmax window_n = np.hanning(N) window_m = np.hamming(N) window_b = np.blackman(N) x = np.arange(0,N,1) #横軸 |
窓関数は計算上に信号の振幅を下げていますので、振幅の値を気にするような分析では、これを補正してあげることが必要です。
その補正値は窓関数の種類によって、変わってきますが、プログラム上では次のように計算させることができます。
|
1 2 3 |
#窓関数の補正値 acf=1/(sum(window_n)/N) F_abs_amp = acf*F_abs_amp #FFT後の数値に掛ければOK |
Python実装したFFT
上記の内容を実装したpythonコードが下記です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 |
############################### #FFT.py #入力された時系列データ(t, x)とサンプリングレート(dt)を元にFFTを行って、 #それを時系列とともにplotする。 ############################### import numpy as np import matplotlib.pyplot as plt def FFT_main(t, x, dt, split_t_r, overlap, window_F, output_FN, y_label, y_unit): #データをオーバーラップして分割する。 split_data = data_split(t, x, split_t_r, overlap) #FFTを行う。 FFT_result_list = [] for split_data_cont in split_data: FFT_result_cont = FFT(split_data_cont, dt, window_F) FFT_result_list.append(FFT_result_cont) """ #各フレームのグラフ化 IDN = 0 for split_data_cont, FFT_result_cont in zip(split_data, FFT_result_list): IDN = IDN+1 plot_FFT(split_data_cont[0], split_data_cont[1], FFT_result_cont[0], FFT_result_cont[1], output_FN, IDN, 0, y_label, y_unit) """ #平均化 fq_ave = FFT_result_list[0][0] F_abs_amp_ave = np.zeros(len(fq_ave)) for i in range(len(FFT_result_list)): F_abs_amp_ave = F_abs_amp_ave + FFT_result_list[i][1] F_abs_amp_ave = F_abs_amp_ave/(i+1) plot_FFT(t, x, fq_ave, F_abs_amp_ave, output_FN, "ave", 1, y_label, y_unit) return fq_ave, F_abs_amp_ave def plot_FFT(t, x, fq, F_abs_amp, output_FN, IDN, final_graph, y_label, y_unit): fig = plt.figure(figsize=(12, 4)) ax2 = fig.add_subplot(121) title1 = "time_" + output_FN[:-4] plt.plot(t, x) plt.xlabel("time [s]") plt.ylabel(y_label+"["+y_unit+"]") plt.title(title1) ax2 = fig.add_subplot(122) title2 = "freq_" + output_FN[:-4] plt.xlabel('freqency(Hz)') plt.ylabel(y_label+"["+y_unit+"/rtHz]") plt.xscale("log") plt.yscale("log") plt.plot(fq, F_abs_amp) plt.title(title2) if final_graph == 0: plt.savefig(output_FN[:-4]+"_"+str(IDN)+"_FFTtemp"+output_FN[-4:], dpi=300) elif final_graph == 1: plt.savefig(output_FN, dpi=300) return 0 def FFT(data_input, dt, window_F): N = len(data_input[0]) #窓の用意 if window_F == "hanning": window = np.hanning(N) # ハニング窓 elif window_F == "hamming": window = np.hamming(N) # ハミング窓 elif window_F == "blackman": window = np.blackman(N) # ブラックマン窓 else: print("Error: input window function name is not sapported. Your input: ", window_F) print("Hanning window function is used.") hanning = np.hanning(N) # ハニング窓 #窓関数後の信号 x_windowed = data_input[1]*window #FFT計算 F = np.fft.fft(x_windowed) F_abs = np.abs(F) F_abs_amp = F_abs / N * 2 fq = np.linspace(0, 1.0/dt, N) #窓補正 acf=1/(sum(window)/N) F_abs_amp = acf*F_abs_amp #ナイキスト定数まで抽出 fq_out = fq[:int(N/2)+1] F_abs_amp_out = F_abs_amp[:int(N/2)+1] return [fq_out, F_abs_amp_out] def data_split(t, x, split_t_r, overlap): split_data = [] one_frame_N = int(len(t)*split_t_r) #1フレームのサンプル数 overlap_N = int(one_frame_N*overlap) #オーバーラップするサンプル数 start_S = 0 end_S = start_S + one_frame_N while True: t_cont = t[start_S:end_S] x_cont = x[start_S:end_S] split_data.append([t_cont, x_cont]) start_S = start_S + (one_frame_N - overlap_N) end_S = start_S + one_frame_N if end_S > len(t): break return np.array(split_data) if __name__ == "__main__": t = np.arange(0.1, 100.0, 0.01) x = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t) dt = 0.01 #This value should be correct as real. output_FN = "test.png" split_t_r = 0.1 #1つの枠で全体のどの割合のデータを分析するか。 overlap = 0.5 #オーバーラップ率 window_F = "hanning" #窓関数選択: hanning, hamming, blackman y_label = "amplitude" y_unit = "V" FFT_main(t, x, dt, split_t_r, overlap, window_F, output_FN, y_label, y_unit) |
if __name__ == “__main__”: のブロックの内容を変えてあげればいろいろ遊べます。
上記のコードの例では、10Hzと20Hzのsin波を足し合わせた信号を入力信号としています。
ですのでその結果は次のようになります。
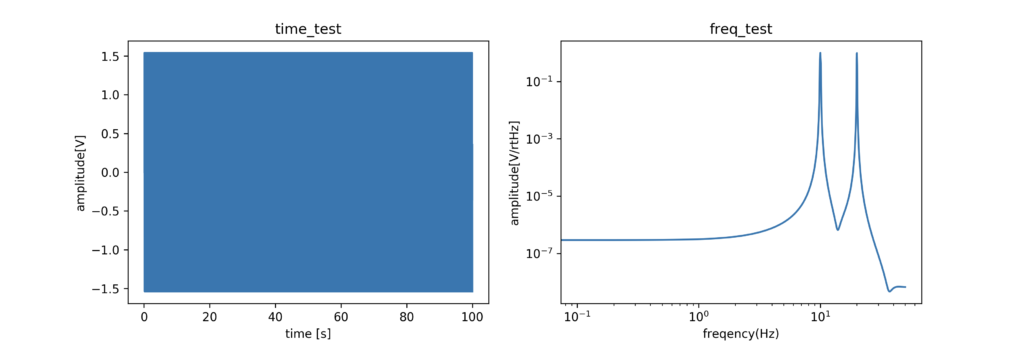
左図の時間グラフでは、潰れて何も見えないですが、10Hzと20Hzの合成波です。右図ではちゃんと10Hzと20Hzにピークが見えていますね。
またよくみるとわかりますが、そのピークの頂点は1になっています。これは窓関数を掛けているものの、補正をちゃんと行っているからです。
窓関数を変えると少々結果のグラフは変化します。
どの窓関数を選択するかはどのような信号を見ているかによるようですが、hanningにしておけばほとんどの場合、問題ないようです。
最後に
pythonでFFTを行うこと自体は簡単なんですが、実際に使用するには、オーバーラップ処理と呼ばれる周波数分解能を犠牲にしたノイズ低減処理や、つなぎ合わせ処理による影響を低減するために窓関数処理が必要です。
今回はそこも含めてpythonでのFFT計算のやり方を紹介しました。
どうぞご参考まで！
コメント