新幹線は空を飛べるのか？窓が開けられない理由がここに？

今回は、新幹線から乗客が全員手を外に出した場合に得られる浮力を計算してこれによって新幹線が空を飛ぶにはどれだけの速度が必要かを計算してみました。

新幹線が空を飛ぶには？

まず、乗客を座席に縛り上げます。

その状態で、飛行機の翼みたいに、手のひらを斜め45度にして窓から外に出してもらう。

走行している新幹線なら、風が手のひらにあたり、下方向に風を受け流すことになる。

風、つまり空気分子を下向きに流すということは、その反動(=反作用)が手に加わるので、手( = 乗客 = 新幹線)は上向きの力がかかる。

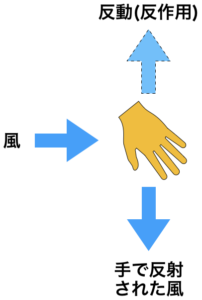
なので原理的には、その風の力で、空を飛べるはず。

ただし、新幹線の走行速度と、乗客の体重も含めた新幹線の質量によって飛べるかどうかが変わってくる。

条件と計算モデル

下記の図のように、新幹線の全ての窓から手が出ているとしてそれによって得られる浮力を計算する。

新幹線は最新モデルのN700Sを仮定すると、

乗客、空気に対する条件は下記

図1における、反射された風によって得られた反作用(力)はベルヌーイの定理を使って計算する。(乱流は無視し、空気は手に対して完全弾性衝突するとする。)

つまり1つの手(面積\( A_h \) )で得られる上向きの力(\( f \) )は、下記のように計算できる。

$$ f = \frac{1}{2}\rho v^2 A_h $$

ここで\( \rho \)は空気の密度で、\( v \)は空気の速さ、つまりは新幹線の速さとなる。

この力が、窓の数(\( N_w \) )だけ合わさって、それが新幹線の質量( \( M \) )と全乗客の質量( \( m \) )を支えられれば、新幹線は飛べることになる。

式にすると下記のようになる。

$$ f\times N_w = (M+m)g $$

ここでgは重力加速度定数で\( 9.8 m/s^2 \)である。

上記の2つの式を合わせて、新幹線の速度\( v \) について解くと次のようになる。

$$ \frac{1}{2}\rho v^2 A_h N_w = (M+m)g \\ v = \sqrt{\frac{2(M+m)g}{A_hN_w\rho}} $$

これが新幹線を空に飛ばすために必要なギリギリの速度となる。

計算結果→マッハ2.3あれば新幹線は飛べる。

上記の式に値を放り込んでいく。

$$ v = \sqrt{\frac{2(M+m)g}{A_hN_w\rho}} \\ = \sqrt{\frac{2 \cdot (7\times 10^5+1\times 10^5)\cdot 9.8}{0.03\cdot 600 \cdot 1.3}} \\ = 819 \left[ {\rm \frac{m}{s}} \right] $$

つまり、新幹線が800 m/s = 時速2880kmの速度で走行すれば空が飛べることになる。

マッハ2.3である。