こんにちは、おはようございます、こんばんは、理系夫婦の夫たんたん(@rikeifufu_otto)です!
誰もが、普段の日常生活を営んでいくと「ラグランジュ方程式」をよく耳にすると思いますが、
最小作用原理からの導出や、ハミルトン方程式との関係性、「一般化された」使い方は、よく見るけど具体的な使い方は?これを使うと何が嬉しいの?
という様な感想をお持ちだと思います。
ラグランジュ方程式の導出やその結果から得られる「一般的な」考察は教科書にお任せして、今回はその便利さや使い方について具体例で説明してみたいと思います。
ラグランジュ方程式はどの様な道具か
まずはこの道具の使い方説明が必要です。
どの様な道具で、どの様に使ったら、どの様に便利なのか。
そう、T-falのポッドと同じ。
T-falのポッドは、ヤカンを超絶可愛くした形をしていて、水を入れてスイッチをONすると、あら不思議すぐにお湯になる。火を使わず、安全で、好きな時に好きな量のお湯がすぐに得られる便利さが特徴。
ラグランジュ方程式に話を戻すと、まずはそれがどういう道具なのか。
ラグランジュ方程式は下記の最小作用の原理から導かれる方程式である。
最小作用の原理: 系は作用と呼ばれる次の値\( S \)を最小にする様に、動く。
$$ S=\int_{t_1}^{t_2} L(q, \dot{q}, t) {\rm d}t \ \ \ \ ({\rm eq.1})$$
ここで\( q, \dot{q} \)は一般化された位置(複数粒子ならそれぞれの位置になる)とその時間微分である。
原理なので、証明はできないけど、実験事実と矛盾しない。
上記の式をあ〜だ、こうだと変形していくと、下記のラグランジュ方程式が導ける。
ラグランジュ方程式
$$ \frac{{\rm d}}{{\rm d}t} \frac{{\rm \partial}L}{{\partial}\dot{q}} – \frac{{\rm \partial}q}{{\rm \partial}t} = 0 \ \ \ \ ({\rm eq.2})$$
ここで\( L \)は運動エネルギー\( T \)とポテンシャルエネルギー\( U \)によって次の様な形で表される。
$$ L = T – U \ \ \ \ ({\rm eq.3})$$
これがラグランジュ方程式という道具です。
使い方としては、考えている系(例えば単振り子)の運動エネルギー、ポテンシャルエネルギーをeq.3に入れて、\( L \)を作って、それをeq.2に代入する。
すると、あら不思議、運動方程式が得られる。
 けろたん
けろたん例えば単振り子の運動方程式が得られて何が嬉しんだよ。ブランコ記事の時の様に普通に作ればいいじゃん。



単振り子は超簡単だったけど、2重振り子とか、糸がバネでできている10重振り子の時にも、いちいち力の向きとか、座標とかを考えて、それぞれの質点の運動方程式を考える?



そ、そんな時には、投げ出すにゃん!
にゃんたん的には投げ出せば良いが、皆さんはそうはいかない時が多いだろう。
そんな時にも簡単にほぼ何も考えずに運動方程式が作れるのが、ラグランジュ方程式の良いところです。



ちょっと待ってよ?それって便利なの?ブランコの時は運動方程式を解くのが大変だったじゃん?いろんなHPとか教科書を見て、どの手法がわかりやすくて、天下り的なものが少ないかを調べて、カンニングして記事にしてたじゃん!



あれはあれ。これはこれ。というのも、実際の生活では、あんなふうに数式上で解ける場合は非常に少なく、結局運動方程式と言う名の微分方程式まで落とせれば、あとはコンピュータに解かせてしまう。
実利用例(1): 2重振り子
次に実際の使い方を見ていく。
まず取り上げるのは、このラグランジュ方程式の使い方例としてもっともよく出てくる2重振子の例。
考えている系は次の図のようになっている。
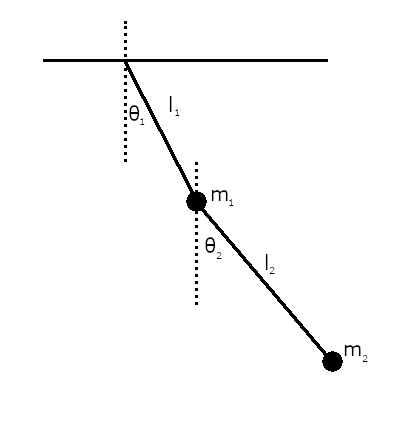

ラグラジアン\( L \)を求めるには、この系の運動エネルギー(\( T = T_1 + T_2 \) )と、ポテンシャルエネルギー( \( U=U_1+U_2 \) )を求めれば良い。
各質点\( m_1, m_2 \)のそれぞれについて考えてみる。
ちなみにポテンシャルエネルギーには基準が必要だが、天井との接触点としよう。(実はこの点にしなくても計算結果は同じ様になるが、計算過程が複雑になってしまう。)
まずは、\( m_1 \)に関して。
これは簡単。
$$ T_1 = \frac{1}{2} m_1 (l_1 \dot{\theta_1})^2 \ \ \ \ ({\rm eq.4}) \\
U_1 = -m_1 g l_1\cos\theta_1 \ \ \ \ ({\rm eq.5}) $$
次は\( m_2 \)に関して。
これはちょっとだけ面倒だけど、なんてことはない。
まずは極座標(\( \theta, l \) )をデカルト座標(\( a, y \) )に直して、計算しやすい様にする。
$$ x_2 = l_1\sin \theta _1 + l_2\sin \theta_2 \\
y_2 = -l_1\cos\theta_1 – l_2\cos\theta_2 $$
これを使ってまずは運動エネルギー\( T_2 \)を求める。
$$ T_2 = \frac{1}{2} m_2 (\dot{x}_2^2 + \dot{y}_2^2) \\
=\frac{m_2}{2} \left[ (l_1\cos \theta_1 \dot{\theta}_1 + l_2\cos \theta_2 \dot{\theta}_2)^2 + (-1)^2(-l_1\sin\theta_1\dot{\theta}_1 – l_2\sin\theta_2\dot{\theta}_2)^2 \right] \\ = \frac{m_2}{2}\left[ l_1^2\cos^2 \theta_1\dot{\theta}_2^2 + 2l_1l_2\cos\theta_1\cos\theta_2\dot{\theta}_1\dot{\theta}_2 + l_2^2\cos^2\theta_2\dot{\theta}_2^2 + l_1^2\sin^2\theta_1\dot{\theta}_1^2 + 2l_1l_2\sin\theta_1\sin\theta_2\dot{\theta}_1\dot{\theta}_2 +l_2^2\sin^2\theta_2\dot{\theta}_2^2 \right] \\ = \frac{m_2}{2}\left[ l_1^2\dot{\theta}_1^2 + 2l_1l_2\dot{\theta}_1\dot{\theta}_2(\cos\theta_1\cos\theta_2 + \sin\theta_1\sin\theta_2) + l_2^2\dot{\theta}_2^2 \right] \\ =\frac{m_2}{2}\left[ l_1^2\dot{\theta}_1^2 + l_2^2\dot{\theta}_2^2 + 2l_1l_2\dot{\theta}_1 \dot{\theta}_2cos(\theta_1 – \theta_2)\right] \ \ \ \ ({\rm eq.6}) $$
以上でラグラジアンを作る材料が揃った。
あとはeq.3に代入すれば良い。
$$L=T-U \\ = T_1 + T_2 – U_1 – U_2 \\ = \frac{m_1}{2}l_1^2\dot{\theta}_1^2 + \frac{m_2}{2} \left[ l_1^2\dot{\theta}_1^2 + l_2^2\dot{\theta}_2^2 + 2l_1l_2\dot{\theta}_1\dot{\theta}_2\cos(\theta_1-\theta_2) \right] + m_1gl_1\cos\theta_1 + m_2g(l_1\cos\theta_1 + l_2\cos\theta_2) \\ =\frac{m_1 + m_2}{2} l_1^2\dot{\theta}_1^2 + \frac{m_2}{2}l_2^2\dot{\theta}_2^2 + m_2l_1l_2\dot{\theta}_1\dot{\theta}_2\cos(\theta_1-\theta_2) + (m_1+m_2)gl_1\cos\theta_1 + m_2gl_2\cos\theta_2 $$
これが2重振動子のラグラジアンとなる。
では、上記の\( L \)をeq.2に代入して運動方程式を導出してみる。
自由度は2つ(\( \theta_1, \theta_2 \))あるので、それぞれについて運動方程式がたつ。
まずは\( \theta_1 \)について。
$$ \frac{{\rm d}}{{\rm d}t} \frac{{\rm \partial}L}{{\partial}\dot{\theta}_1} – \frac{{\rm \partial}\theta_1}{{\rm \partial}t} =0 \\ \Rightarrow \frac{{\rm d}}{{\rm d}t}\left[ (m_1+m_2)l_1^2\dot{\theta}_1 + m_2l_1l_2\dot{\theta}_2\cos(\theta_1 – \theta_2) \right] – \dot{\theta}_1 = 0 $$
次に\( \theta_2 \)について。
$$ \frac{{\rm d}}{{\rm d}t} \frac{{\rm \partial}L}{{\partial}\dot{\theta}_2} – \frac{{\rm \partial}\theta_2}{{\rm \partial}t} =0 \\ \Rightarrow \frac{{\rm d}}{{\rm d}t}\left[ m_2l_2^2\dot{\theta}_2 + m_2l_1l_2\dot{\theta}_1\cos(\theta_1 – \theta_2) \right] – \dot{\theta}_2 = 0 $$
以上の2つが解くべき運動方程式で、これをコンピュータに解かせると、ある適当な初期条件かでの2重振子の2つの質点の位置を表す角度(\( \theta_1, \theta_2 \))が計算でき、どう動くかがわかります。
実利用例(2): 平面上を回る質点と落ちる質点系
次にもう少しTexが簡単な系を考えてみる。
次の図の様な系を考える。
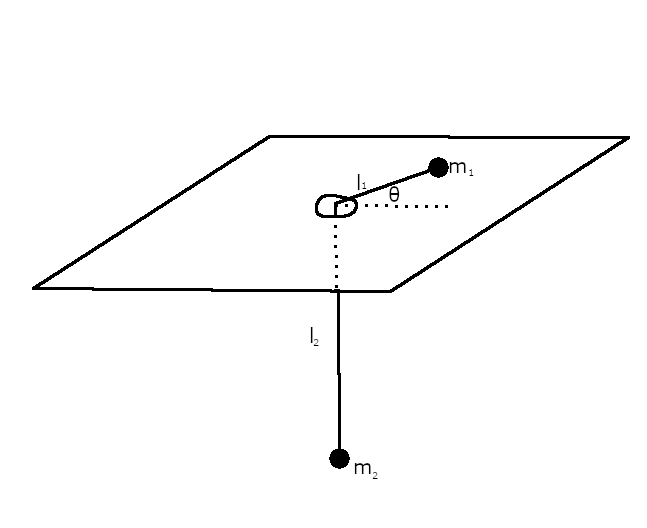

この系では、\( m_1 \)の質点が初速度\( v_0 \)を持った時にそれぞれの質点の運動がどうなるかという問題。
これは先と比べるとかなり簡単。
先と同様に各質点の運動エネルギー、ポテンシャルエネルギーを考えれば良い。
ポテンシャルエネルギーの基準は平面上とする。
まずは\( m_1 \)に関して。
$$ T_1 = \frac{1}{2}m_1(\dot{l}_1^2 + (l_1\dot{\theta})^2) \\ U_1 = 0 $$
次に、\( m_2 \)に関して。
$$ T_2 = \frac{1}{2}m_2\dot{l}_2^2 \\ U_2 = -m_2gl_2 $$
あ、これでできた。
あとはeq.3に代入すれば良い。
$$ L = T – U \\ T_1 + T_2 – U_1 -U_2 \\ = \frac{m_1}{2} \dot{l}_1^2 + \frac{m_2}{2}\dot{l}_2^2 + \frac{m_1}{2}l_1^2\dot{\theta}^2 + m_2gl_2 $$
ラグラジアンが求まれば、あとはラグランジュ方程式eq.2に代入するだけで、運動方程式が導出でき、それは適当にコンピュータで解くことができる。
以上です。
備考
ちなみに上の一番長い式を書くのに下記の様なtexを書かなければならず、もううんざりです。。。




















コメント