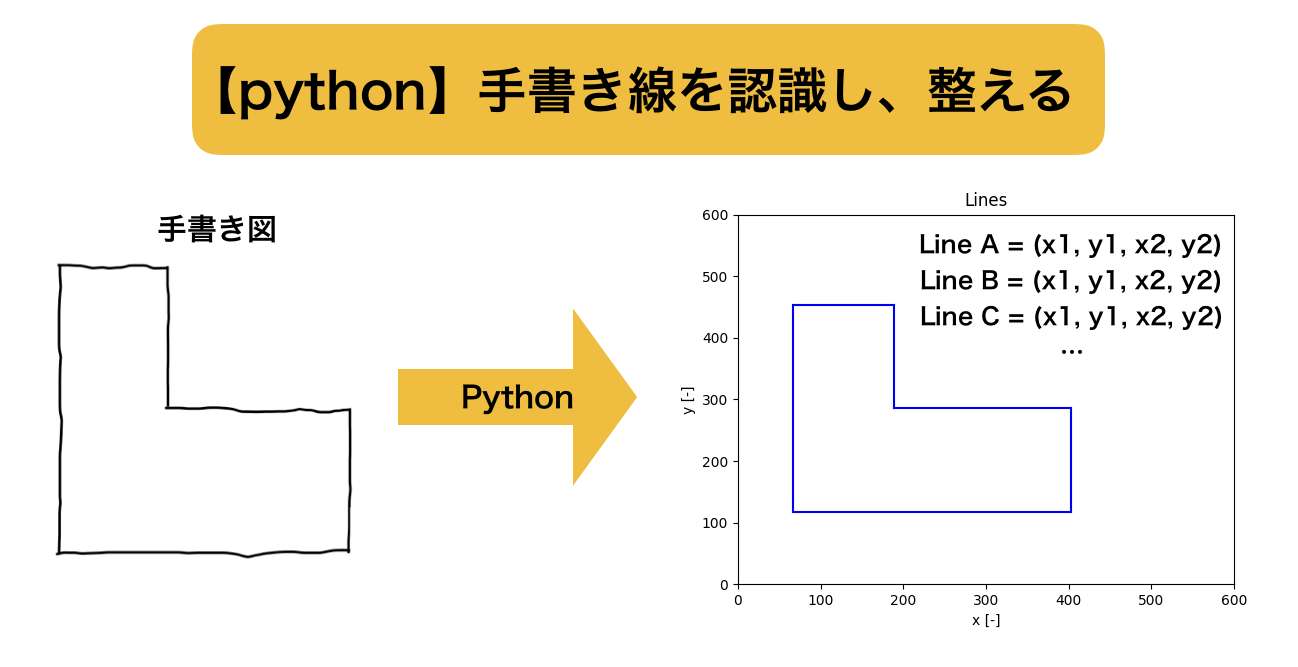
今日は手書きされた図面を、pythonを使用して直線の認識、整理を行い、きっちり並べる手法を紹介します。
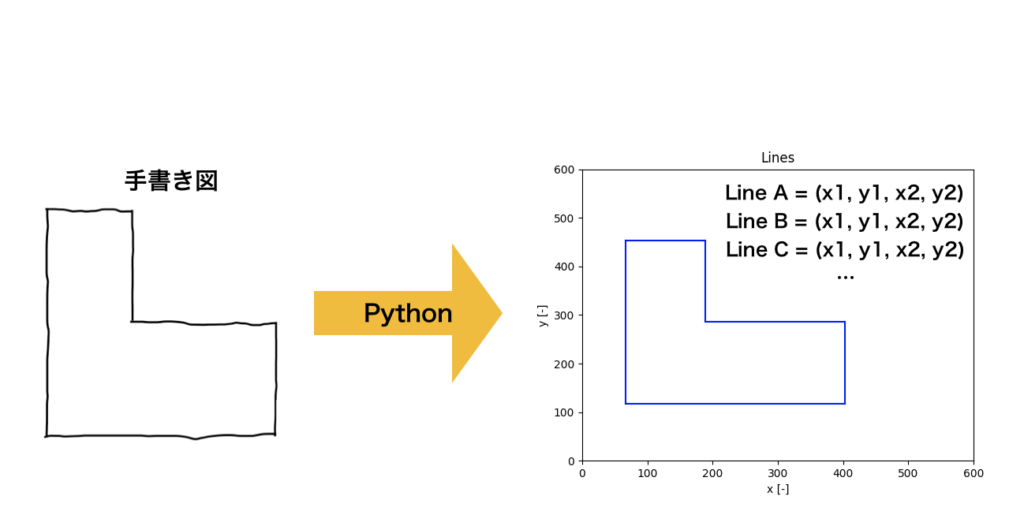
手書き図が少し曲がっていても、線の繋ぎが甘くても、それを整えて右図のようにxy軸に平行できっちりした図に変換します。もちろん各直線の始点終点の座標も出力可能です。
概要: 直線の取得 → 軸平行処理 → 重複線処理 → 端点処理
今回のプログラムの概要を図にしましました。
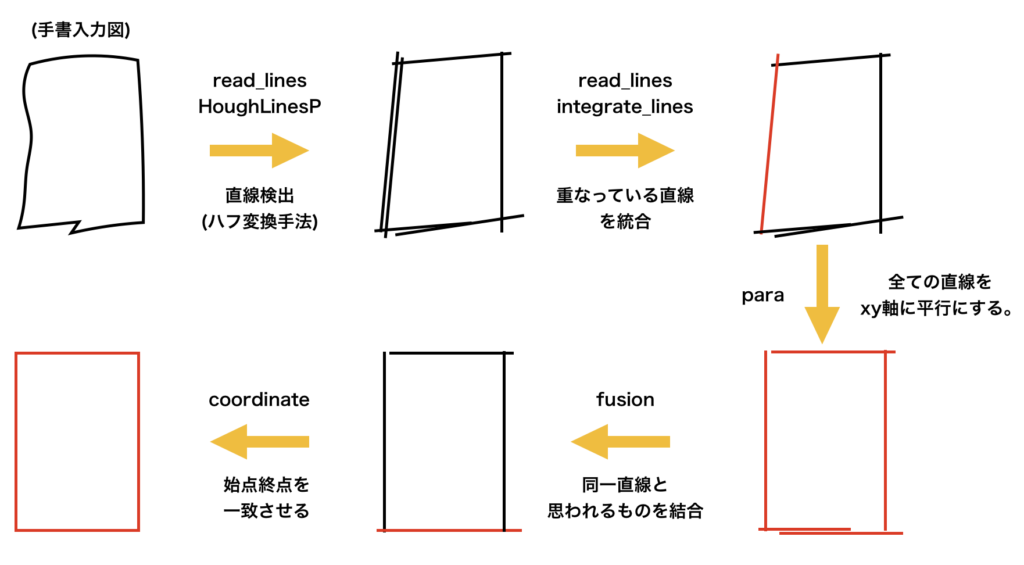
上図には処理内容の説明と共に下記で紹介するコード内の関数名も同時に記載しました。
- openCVを利用した直線検出(ハフ変換手法)でまずは直線を検出
- 手書き線画太かったりすると、同じ線が2本認識されてしまうことがあるので、この重なりを解消
- 全ての線をxy軸に平行になるように整える
- 1つの直線が2本に切れて認識されることもあるので、これを統合された1つの直線にする
- 最後に各直線の端点(始点or終点)を他の直線の端点と一致させる
ソースコードは、メイン関数(digi_conv_main)が、サブ関数(read_lines, para, fusion, coordinate)を順番に呼ぶ構造になっています。最後にplot_lines関数を何回か呼び出し、中間処理結果も含めたグラフ化を行っています。
サブ関数read_linesとfusionは、さらにそれぞれintegrate_lines、fusion_linesを呼び出すようになっています。
以後の説明はpythonのソースコード内で示していきます。
メイン関数(digi_conv_main)
#digi_conv_main
def digi_conv_main():
print("Diigtal conversion prosecc is working...")
#直線の始点終点を揃える範囲[pixel]
merge_r = 10.0
#入力ファイル
input_FN = "intput_fig.png"
#画像のサイズを取得する。
img = cv2.imread(input_FN, cv2.IMREAD_COLOR)
height, width = img.shape[:2] #入力画像の縦、横の大きさ
size = (height + width)/2 #入力画像の大まかな大きさ。点の重なり判断の指標に使われる。
#画像から直線を取得する。
ori_lines = read_lines(input_FN, height)
#取得した直線を全て、x軸に平行もしくはy軸に平行な直線に直す。
para_lines = para(ori_lines)
#重なっている線を結合する。
fuse_lines = fusion(para_lines, size)
#統合された線の両端を揃える。
coor_lines = coordinate(fuse_lines, merge_r)
#このcoor_linesの中身が整えられた最終的な直線群
#直線群のデータ構造: [[x1, y1, x2, y2], [x1, y1, x2, y2], [x1, y1, x2, y2], ...]
#各直線が配列内に順番に並んでいて、それぞれの中では始点終点の座標が格納されている。
#下記はplot処理
#読み取った線をplot
FN = "output_original.png"
plot_lines(ori_lines, FN)
#平行にした線をplot
FN = "output_para.png"
plot_lines(para_lines, FN)
#結合した線をplot
FN = "output_fuse.png"
plot_lines(fuse_lines, FN)
#両端を整えた線をplot
FN = "output_coor.png"
plot_lines(coor_lines, FN)
return 0コード内の「<」は「<」と置き換えてください。
直線検出(認識)関数(read_lines + integrate_lines)
#read_lines + integrate_lines
def read_lines(input_FN, height):
#画像から直線を取得する。
#
#詳細###
#openCVを使って、入力画像に次の処理を行う。
# 1. [画像処理] 画像の読み取り
# 2. [画像処理] カラーデータをグレーデータに変換
# 3. [画像処理] 直線検出の準備として、白黒を反転させる。
# 4. [画像処理] 直線検出(ハフ変換による直線検出)
# 5. [数値処理] 同直線の統合: 始点終点が、他の線と近ければ、統一する。
#height = parameter["height"]
#読み取り
img = cv2.imread(input_FN)
#グレーに変換
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#白黒反転
gray_2 = cv2.bitwise_not(gray)
#直線検出
bare_lines = cv2.HoughLinesP(gray_2, rho=1, theta=np.pi/180, threshold=80, minLineLength=50, maxLineGap=5)
#直線群のデータ構造: [[x1, y1, x2, y2], [x1, y1, x2, y2], [x1, y1, x2, y2], ...]
#各直線が配列内に順番に並んでいて、それぞれの中では始点終点の座標が格納されている。
#同直線の統合
line_p_size = 10
threshold_size = 10
ori_lines_bare = integrate_lines(bare_lines, threshold_size)
ori_lines = []
for line in ori_lines_bare:
line_cont = line[0]
ori_lines.append([line_cont[0], height-line_cont[1], line_cont[2], height-line_cont[3]])
return ori_lines
def integrate_lines(bare_lines, threshold_size):
#同一の直線と思われる直線を統合する。
#詳細###
#入力された直線群の中から、直線を一個ずつ選び、他の直線と比較
#始点終点が他と近くなければ、新規直線としてint_linesに格納していく。
#最終的には、int_lines内に格納された直線同士は、始点終点が互いに異なる。
ori_lines = []
for bare_lines_cont in bare_lines:
for int_lines_cont in ori_lines:
#2直線の始点と終点の差分d1, d2を算出して、それが共に指定距離よりも近くにあるかどうかで、同じ直線かどうかを判断する。
d1 = math.sqrt((int_lines_cont[0][0] - bare_lines_cont[0][0])**2 + (int_lines_cont[0][1] - bare_lines_cont[0][1])**2)
d2 = math.sqrt((int_lines_cont[0][2] - bare_lines_cont[0][2])**2 + (int_lines_cont[0][3] - bare_lines_cont[0][3])**2)
if d1 < threshold_size and d2 < threshold_size:
#同じ直線だと判断した場合
break
else:
#同じ直線がまだint_linesの中にない場合には、新規直線として追加する。
ori_lines.append(bare_lines_cont)
return ori_linesコード内の「<」は「<」と置き換えてください。
直線をxy軸対して平行にする関数(para)
#para
def para(int_lines):
#全ての直線をx,y軸に平行にする。
#詳細###
# 0. 直線群に対して1つずつ処理を行う。
# 1. 縦線か横線かを判断
# 2. 縦線ならxを、横線ならyを始点終点で一致させる。
# 3. 斜め線の場合には警告
# 4. 返り値は座標軸平行に整えられた直線(の始点終点座標)群
para_lines = [] #座標軸に対して平行に整えられた直線が格納される。
for line_cont in int_lines:
x1, y1, x2, y2 = line_cont
#縦か横かの判断を行い、座標を整える。
dx = abs(x1-x2)
dy = abs(y1-y2)
if dx < dy: #縦線
x_out_1 = (x1+x2)/2
x_out_2 = x_out_1
y_out_1 = y1
y_out_2 = y2
else: #横線
x_out_1 = x1
x_out_2 = x2
y_out_1 = (y1+y2)/2
y_out_2 = y_out_1
#斜めの線の時には警告する。
if abs(dx-dy)/((dx+dy)/2) < 0.5:
print("There is a diagonal line!!!")
para_lines.append([x_out_1, y_out_1, x_out_2, y_out_2])
return para_linesコード内の「<」は「<」と置き換えてください。
同一直線の結合を行う関数(fusion)
#fusion + fusion_lines
def fusion(para_lines, size):
#各直線が、他の直線と重なっているかを確認し、
#重なっていれば、融合する。
#size = (height + width)/2
fuse_lines = [] #結合された直線が格納される。
fused_list = []
for line_n in range(len(para_lines)):
if line_n in fused_list:
continue
new_line = copy.copy(para_lines[line_n])
for line_n_n in range(len(para_lines)):
if line_n != line_n_n:
new_line, fusion_switch = fusion_lines(new_line, para_lines[line_n_n], size)
if fusion_switch == 1: #2直線が結合された場合
fused_list.append(line_n_n)
fuse_lines.append(new_line)
return fuse_lines
def fusion_lines(lineA, lineB, size):
#2つの直線の方向を確認し、違う方向ならlineAを返し、
#同じ方向なら、lineAとlineBが重なっているかを確認し、
#重なっていればlineAを返し、重なっていれば2直線を融合してつなぎ合わせる。
#直線の返り値と共に、結合したかどうかを0/1で返す。
#2つの線が同じ方向かの確認
#方向が違えば、lineAを返して終了
if lineA[0] == lineA[2]:
A_angle = "x"
else:
A_angle = "y"
if lineB[0] == lineB[2]:
B_angle = "x"
else:
B_angle = "y"
if A_angle != B_angle:
return lineA, 0
#方向が同じ場合に、直線が重なっているかを確認
if A_angle == "x":
distance = abs(lineA[0] - lineB[0])
pA = [min(lineA[1], lineA[3]), max(lineA[1], lineA[3])]
pB = [min(lineB[1], lineB[3]), max(lineB[1], lineB[3])]
else:
distance = abs(lineA[1] - lineB[1])
pA = [min(lineA[0], lineA[2]), max(lineA[0], lineA[2])]
pB = [min(lineB[0], lineB[2]), max(lineB[0], lineB[2])]
if distance > size/100: #もしも2つの線が十分に離れていれば、lineAを返して終了
return lineA, 0
if pA[0] > pB[1] or pB[0] > pA[1]: #重なっていなければ、lineAを返して終了
return lineA, 0
#ここまで処理が回った=2つの直線は重なっているため、
#直線の方向(x軸に平行か、y軸に平行か)に応じて、融合する。
#融合時には、2直線を足し合わせたようにする。
if A_angle == "x":
x = (lineA[0] + lineA[2] + lineB[0] + lineB[2])/4
y1 = min(lineA[1], lineA[3], lineB[1], lineB[3])
y2 = max(lineA[1], lineA[3], lineB[1], lineB[3])
new_line = [x, y1, x, y2]
else:
y = (lineA[1] + lineA[3] + lineB[1] + lineB[3])/4
x1 = min(lineA[0], lineA[2], lineB[0], lineB[2])
x2 = max(lineA[0], lineA[2], lineB[0], lineB[2])
new_line = [x1, y, x2, y]
return new_line, 1コード内の「<」は「<」と置き換えてください。
直線の端点(始点終点)を一致させる関数(coodinate)
#coodinate
def coordinate(fuse_lines, merge_r):
#各直線の始点終点座標を、近い点で揃える。
#そろえる範囲をcoor_dで指定する。
in_lines = copy.deepcopy(fuse_lines)
for i, line in enumerate(in_lines):
for k in [0,2]: #x軸方向 in_lines[i][k]の全てを回す。
for j, line_cont in enumerate(in_lines):
for g in [0,2]:
if i==j and k==g: continue
if abs(line[k] - line_cont[g]) < merge_r:
in_lines[j][g] = line[k]
for k in [1,3]: #y軸方向 in_lines[i][k]の全てを回す。
for j, line_cont in enumerate(in_lines):
for g in [1,3]:
if i==j and k==g: continue
if abs(line[k] - line_cont[g]) < merge_r:
in_lines[j][g] = line[k]
return in_linesコード内の「<」は「<」と置き換えてください。
plotを行う関数(plot_lines)
#plot_lines
def plot_lines(lines, FN):
#入力された直線をグラフにplotする。
fig = plt.figure()
plt.xlim(0, 600)
plt.ylim(0, 600)
plt.xlabel("x [-]")
plt.ylabel("y [-]")
plt.title("Lines")
#取得した直線のplot
for line_cont in lines:
x = [line_cont[0], line_cont[2]] #[始点座標、終点座標]
y = [line_cont[1], line_cont[3]] #[始点座標、終点座標]
plt.plot(x, y, color="blue")
#画像として保存する。
fig.savefig(FN)
return 0コード内の「<」は「<」と置き換えてください。
全てを1つのpythonファイルに書いた場合(コピペ実行可能)
ここでは上記で紹介した関数を1つのファイルに書き、実行できる形を示します。
#digital_conversion.py
#digital_conversion.py
# 2020/3/10
# Tan Tan
#
#手書きの画像データから図面を起こす。
import cv2
import numpy as np
import math
import matplotlib
import matplotlib.pyplot as plt
import copy
def digi_conv_main():
print("Diigtal conversion prosecc is working...")
#直線の始点終点を揃える範囲[pixel]
merge_r = 10.0
#入力ファイル
input_FN = "intput_fig.png"
#画像のサイズを取得する。
img = cv2.imread(input_FN, cv2.IMREAD_COLOR)
height, width = img.shape[:2] #入力画像の縦、横の大きさ
size = (height + width)/2 #入力画像の大まかな大きさ。点の重なり判断の指標に使われる。
#画像から直線を取得する。
ori_lines = read_lines(input_FN, height)
#取得した直線を全て、x軸に平行もしくはy軸に平行な直線に直す。
para_lines = para(ori_lines)
#重なっている線を結合する。
fuse_lines = fusion(para_lines, size)
#統合された線の両端を揃える。
coor_lines = coordinate(fuse_lines, merge_r)
#このcoor_linesの中身が整えられた最終的な直線群
#直線群のデータ構造: [[x1, y1, x2, y2], [x1, y1, x2, y2], [x1, y1, x2, y2], ...]
#各直線が配列内に順番に並んでいて、それぞれの中では始点終点の座標が格納されている。
#下記はplot処理
#読み取った線をplot
FN = "output_original.png"
plot_lines(ori_lines, FN)
#平行にした線をplot
FN = "output_para.png"
plot_lines(para_lines, FN)
#結合した線をplot
FN = "output_fuse.png"
plot_lines(fuse_lines, FN)
#両端を整えた線をplot
FN = "output_coor.png"
plot_lines(coor_lines, FN)
return 0
def read_lines(input_FN, height):
#画像から直線を取得する。
#
#詳細###
#openCVを使って、入力画像に次の処理を行う。
# 1. [画像処理] 画像の読み取り
# 2. [画像処理] カラーデータをグレーデータに変換
# 3. [画像処理] 直線検出の準備として、白黒を反転させる。
# 4. [画像処理] 直線検出(ハフ変換による直線検出)
# 5. [数値処理] 同直線の統合: 始点終点が、他の線と近ければ、統一する。
#height = parameter["height"]
#読み取り
img = cv2.imread(input_FN)
#グレーに変換
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#白黒反転
gray_2 = cv2.bitwise_not(gray)
#直線検出
bare_lines = cv2.HoughLinesP(gray_2, rho=1, theta=np.pi/180, threshold=80, minLineLength=50, maxLineGap=5)
#直線群のデータ構造: [[x1, y1, x2, y2], [x1, y1, x2, y2], [x1, y1, x2, y2], ...]
#各直線が配列内に順番に並んでいて、それぞれの中では始点終点の座標が格納されている。
#同直線の統合
line_p_size = 10
threshold_size = 10
ori_lines_bare = integrate_lines(bare_lines, threshold_size)
ori_lines = []
for line in ori_lines_bare:
line_cont = line[0]
ori_lines.append([line_cont[0], height-line_cont[1], line_cont[2], height-line_cont[3]])
return ori_lines
def integrate_lines(bare_lines, threshold_size):
#同一の直線と思われる直線を統合する。
#詳細###
#入力された直線群の中から、直線を一個ずつ選び、他の直線と比較
#始点終点が他と近くなければ、新規直線としてint_linesに格納していく。
#最終的には、int_lines内に格納された直線同士は、始点終点が互いに異なる。
ori_lines = []
for bare_lines_cont in bare_lines:
for int_lines_cont in ori_lines:
#2直線の始点と終点の差分d1, d2を算出して、それが共に指定距離よりも近くにあるかどうかで、同じ直線かどうかを判断する。
d1 = math.sqrt((int_lines_cont[0][0] - bare_lines_cont[0][0])**2 + (int_lines_cont[0][1] - bare_lines_cont[0][1])**2)
d2 = math.sqrt((int_lines_cont[0][2] - bare_lines_cont[0][2])**2 + (int_lines_cont[0][3] - bare_lines_cont[0][3])**2)
if d1 < threshold_size and d2 < threshold_size:
#同じ直線だと判断した場合
break
else:
#同じ直線がまだint_linesの中にない場合には、新規直線として追加する。
ori_lines.append(bare_lines_cont)
return ori_lines
def para(int_lines):
#全ての直線をx,y軸に平行にする。
#詳細###
# 0. 直線群に対して1つずつ処理を行う。
# 1. 縦線か横線かを判断
# 2. 縦線ならxを、横線ならyを始点終点で一致させる。
# 3. 斜め線の場合には警告
# 4. 返り値は座標軸平行に整えられた直線(の始点終点座標)群
para_lines = [] #座標軸に対して平行に整えられた直線が格納される。
for line_cont in int_lines:
x1, y1, x2, y2 = line_cont
#縦か横かの判断を行い、座標を整える。
dx = abs(x1-x2)
dy = abs(y1-y2)
if dx < dy: #縦線
x_out_1 = (x1+x2)/2
x_out_2 = x_out_1
y_out_1 = y1
y_out_2 = y2
else: #横線
x_out_1 = x1
x_out_2 = x2
y_out_1 = (y1+y2)/2
y_out_2 = y_out_1
#斜めの線の時には警告する。
if abs(dx-dy)/((dx+dy)/2) < 0.5:
print("There is a diagonal line!!!")
para_lines.append([x_out_1, y_out_1, x_out_2, y_out_2])
return para_lines
def fusion(para_lines, size):
#各直線が、他の直線と重なっているかを確認し、
#重なっていれば、融合する。
#size = (height + width)/2
fuse_lines = [] #結合された直線が格納される。
fused_list = []
for line_n in range(len(para_lines)):
if line_n in fused_list:
continue
new_line = copy.copy(para_lines[line_n])
for line_n_n in range(len(para_lines)):
if line_n != line_n_n:
new_line, fusion_switch = fusion_lines(new_line, para_lines[line_n_n], size)
if fusion_switch == 1: #2直線が結合された場合
fused_list.append(line_n_n)
fuse_lines.append(new_line)
return fuse_lines
def fusion_lines(lineA, lineB, size):
#2つの直線の方向を確認し、違う方向ならlineAを返し、
#同じ方向なら、lineAとlineBが重なっているかを確認し、
#重なっていればlineAを返し、重なっていれば2直線を融合してつなぎ合わせる。
#直線の返り値と共に、結合したかどうかを0/1で返す。
#2つの線が同じ方向かの確認
#方向が違えば、lineAを返して終了
if lineA[0] == lineA[2]:
A_angle = "x"
else:
A_angle = "y"
if lineB[0] == lineB[2]:
B_angle = "x"
else:
B_angle = "y"
if A_angle != B_angle:
return lineA, 0
#方向が同じ場合に、直線が重なっているかを確認
if A_angle == "x":
distance = abs(lineA[0] - lineB[0])
pA = [min(lineA[1], lineA[3]), max(lineA[1], lineA[3])]
pB = [min(lineB[1], lineB[3]), max(lineB[1], lineB[3])]
else:
distance = abs(lineA[1] - lineB[1])
pA = [min(lineA[0], lineA[2]), max(lineA[0], lineA[2])]
pB = [min(lineB[0], lineB[2]), max(lineB[0], lineB[2])]
if distance > size/100: #もしも2つの線が十分に離れていれば、lineAを返して終了
return lineA, 0
if pA[0] > pB[1] or pB[0] > pA[1]: #重なっていなければ、lineAを返して終了
return lineA, 0
#ここまで処理が回った=2つの直線は重なっているため、
#直線の方向(x軸に平行か、y軸に平行か)に応じて、融合する。
#融合時には、2直線を足し合わせたようにする。
if A_angle == "x":
x = (lineA[0] + lineA[2] + lineB[0] + lineB[2])/4
y1 = min(lineA[1], lineA[3], lineB[1], lineB[3])
y2 = max(lineA[1], lineA[3], lineB[1], lineB[3])
new_line = [x, y1, x, y2]
else:
y = (lineA[1] + lineA[3] + lineB[1] + lineB[3])/4
x1 = min(lineA[0], lineA[2], lineB[0], lineB[2])
x2 = max(lineA[0], lineA[2], lineB[0], lineB[2])
new_line = [x1, y, x2, y]
return new_line, 1
def coordinate(fuse_lines, merge_r):
#各直線の始点終点座標を、近い点で揃える。
#そろえる範囲をcoor_dで指定する。
in_lines = copy.deepcopy(fuse_lines)
for i, line in enumerate(in_lines):
for k in [0,2]: #x軸方向 in_lines[i][k]の全てを回す。
for j, line_cont in enumerate(in_lines):
for g in [0,2]:
if i==j and k==g: continue
if abs(line[k] - line_cont[g]) < merge_r:
in_lines[j][g] = line[k]
for k in [1,3]: #y軸方向 in_lines[i][k]の全てを回す。
for j, line_cont in enumerate(in_lines):
for g in [1,3]:
if i==j and k==g: continue
if abs(line[k] - line_cont[g]) < merge_r:
in_lines[j][g] = line[k]
return in_lines
def plot_lines(lines, FN):
#入力された直線をグラフにplotする。
fig = plt.figure()
plt.xlim(0, 600)
plt.ylim(0, 600)
plt.xlabel("x [-]")
plt.ylabel("y [-]")
plt.title("Lines")
#取得した直線のplot
for line_cont in lines:
x = [line_cont[0], line_cont[2]] #[始点座標、終点座標]
y = [line_cont[1], line_cont[3]] #[始点座標、終点座標]
plt.plot(x, y, color="blue")
#画像として保存する。
fig.savefig(FN)
return 0
if __name__=="__main__":
#メインプログラムの呼び出し
digi_conv_main()
コード内の「<」は「<」と置き換えてください。
入力する図の例も残しておきますので、これで試験していただければ下記と同じような結果が得られるはず!
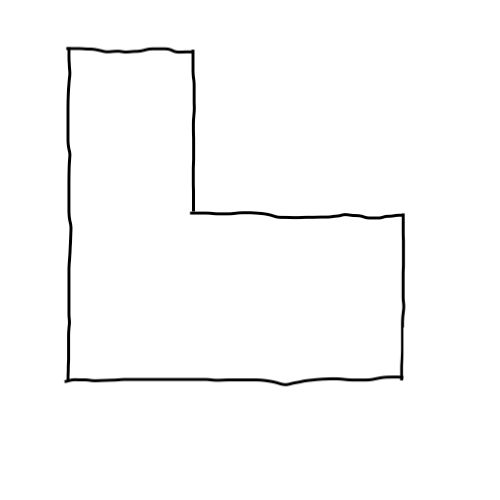
実行結果例
ここに実行結果の例を示したいと思います。
途中経過の図も示しておきます。
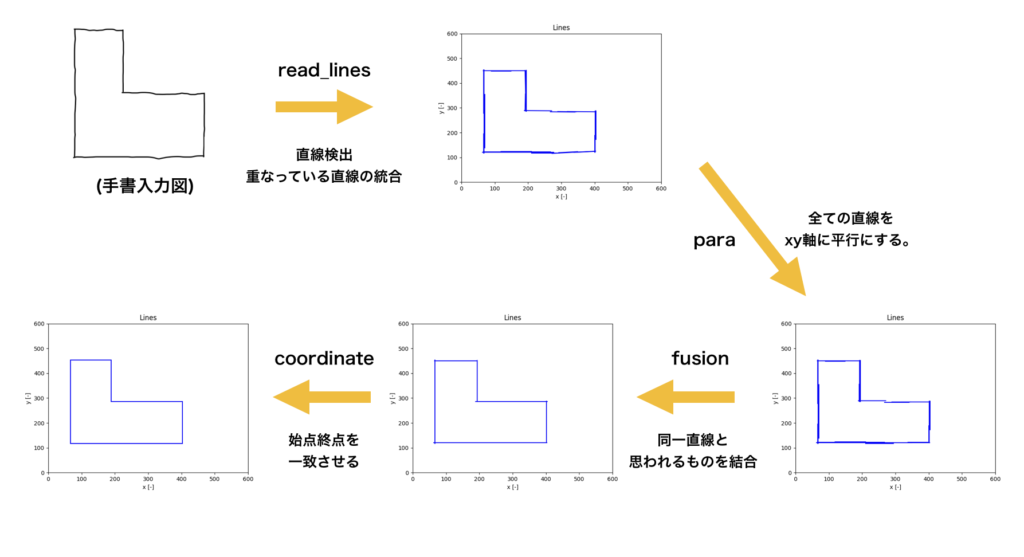
処理された最終的な結果の直線群はdigi_conv_main関数内のcoor_linesの中に座標が格納されていますのでいくらでもデータ処理ができます。
これで手書きされた図面も整えて、好きなようにデータ処理ができます!

















コメント