振り子による防振

防振を考えるための最もシンプルな系: 単振り子

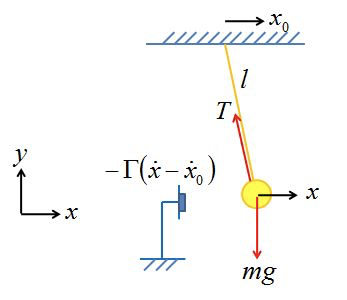
上記の図が単振り子系で、防振したい物体が黄色の球で、天井から吊るされているイメージ。
これによって、天井に撃力が加わっても、黄色の球まで伝わる衝撃を少なくできる。

系の説明。\( x_0 \)が外部振動変位で、\( x \)が質点の変位である。
この質点に対しては、速度に対して、ダンピング(摩擦)が働いており、\( -\Gamma (\dot{x} – \dot{x_0}) \)で表されている。
この項についてもう少し詳しくみると、外部の速度\( \dot{x_0} \)と質点の速度\( \dot{x} \)の差(=外部系に静止した系から見た質点の速度)に比例した負の力が加わっている、と考える。\( \Gamma \)はその比例定数。

並進の\(x\)方向のみを考える。張力\(T\)の\(y\)方向成分\(T_y\)及び\(x\)方向成分\(T_x\)の大きさは、

$$ T_y = T\sqrt{1-\frac{(x-x_0)^2}{l^2}} \simeq T = mg \\
T_x = T\frac{x-x_0}{l} = m\frac{g}{l}(x-x_0) $$

となる。よって質点の\(x\)方向の運動方程式は次の様になる。この時、速度に比例するような抵抗力が働くと仮定した。その大きさは先に説明したように\(\Gamma\)に寄与する。

$$ m\ddot{x} = -\Gamma(\dot{x}-\dot{x}_0) -m\frac{g}{l}(x-x_0) $$

ここで\(x, x_0\)はともに時間の関数である。この微分方程式を解くにあたって、フーリェ変換を使用する。
(フーリエ変換の説明はここでは割愛する。)

$$ -m\omega^2 X = -i\Gamma\omega X +i\Gamma\omega X_0 -m\omega_1^2X + m\omega_1^2X_0 $$

となる。なおここで\( \omega_1\equiv\sqrt{\frac{g}{l}} \)とした。これを解き、防振比\( Z\equiv \frac{X}{X_0} \)を求めると、

$$ \frac{X}{X_0} = \frac{-m\omega_1^2-i\Gamma\omega}{m(\omega^2-\omega_1^2) – i\Gamma\omega} \equiv Z $$

となる。この大きさ\( \left| \frac{X}{X_0} \right| \) :gainと位相\( \phi \)を求めると以下の様になる。

$$ \left| \frac{X}{X_0} \right| = \sqrt{Z\bar{Z}} \\
\phi = \arctan \frac{Im(Z)}{Re(Z)} $$

\( \bar{Z} \)は\( Z \)の複素共役を意味する。これをグラフにする。使用したパラメータは以下である。

$$ m = 1.3 [kg] \\
\omega_1 = \sqrt{\frac{g}{l}} = \sqrt{\frac{9.8}{0.2}} = 7.0 [rad/s] \\
\nu_1 \equiv \frac{\omega_1}{2\pi} = 1.1[Hz] $$

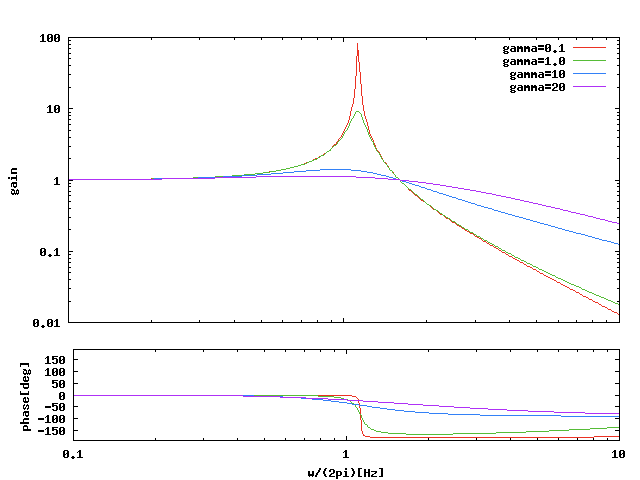
この図は伝達関数と呼ばれる。
外部の振動(\( x_0 \))がどれだけ内部(\( x \))に伝わるかを周波数空間で示している。
例えば外部に0.1Hzの周期的な振動があったとしたら、この単振り子系では、それがそのまま(gain=1)質点まで伝わる。外部振動に10cmの振幅があったとすれば、質点も10cmの振幅で揺れる。
一方でこの振り子の共振周波数(1.1Hz)の外部振動があった場合には、「共振現象」がおきて、振り子がたくさん揺れる。gainが高いということ。
さらに高周波では、gainが0.1などのように1よりも小さくなっているので、その分だけ質点が揺れていないということを示している。

つまり、振り子の共振周波数より高い周波数においては、「防振」が行われる。

どれだけ共振周波数で揺れてしまうかは、\( \Gamma \)の大きさによってくる。
この摩擦が小さければ、共振周波数でたくさん揺れる代わりに共振周波数以上での防振が強くなる。
この摩擦が大きいと、共振周波数では比較的揺れが小さいが、共振周波数以上での防振効果が弱くなる。

ちなみに図中の下部にある図は\( x_0 \)と\( x \)の位相差を示しており、0度は同相(外部が右に揺れて位置していれば、質点も右に位置している)、-180度はちょうど逆位相(外部が右に揺れているなら、質点は左に位置する)になっていることを意味する。