冬休み、ふと、マクスウェル-ボルツマン分布(以下マクスウェル分布)を、基本方程式から導たくなった。
マクスウェル分布
$$ f(v) = \left( \frac{m}{2\pi k_BT} \right)^{\frac{3}{2}}4\pi v^2\exp \left(-\frac{m v^2}{2k_BT} \right) $$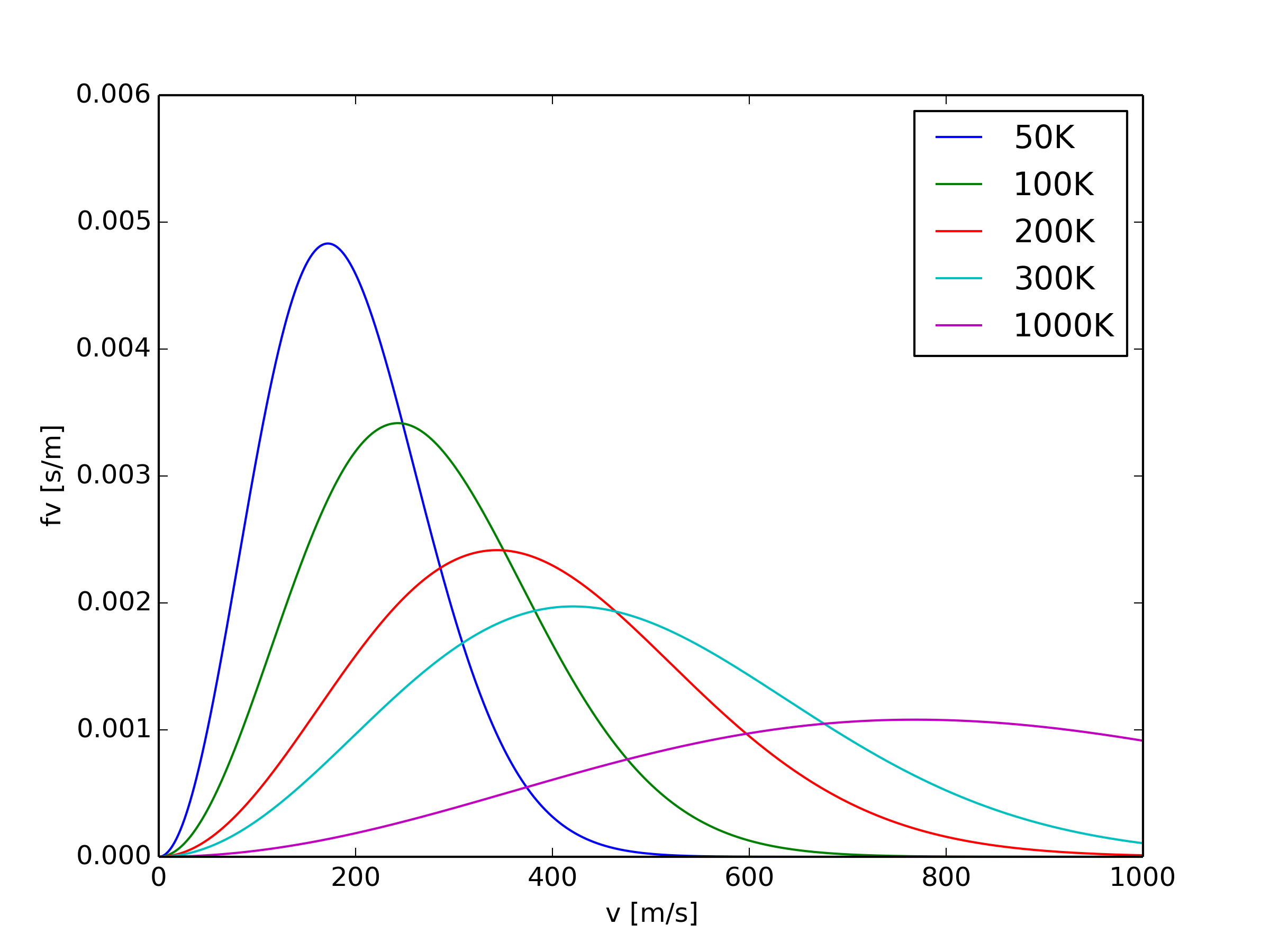
熱平衡状態における気体粒子の速度分布を表しています。
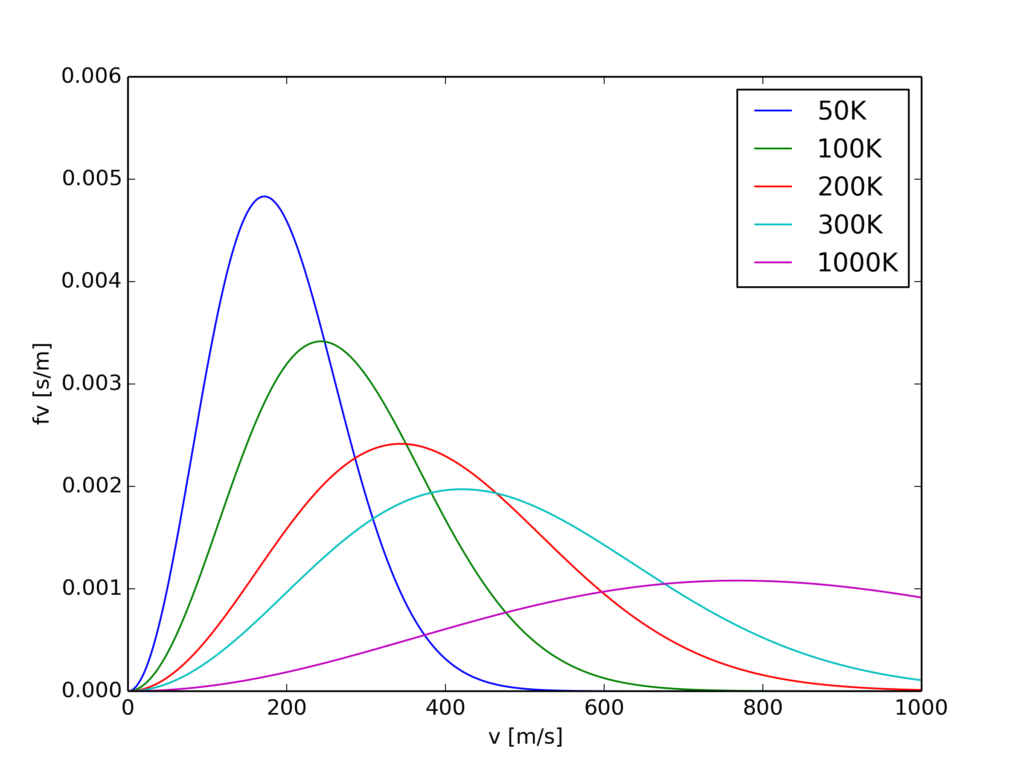
上記グラフは窒素分子を仮定して計算していて、縦軸が速度分布(その速度での粒子の割合/速度)を表しています。各線は横軸ゼロから無限大まで積分を行うと1になります。
今回はこの式を最初から導出してみたいと思います。
概要: 導出の流れ
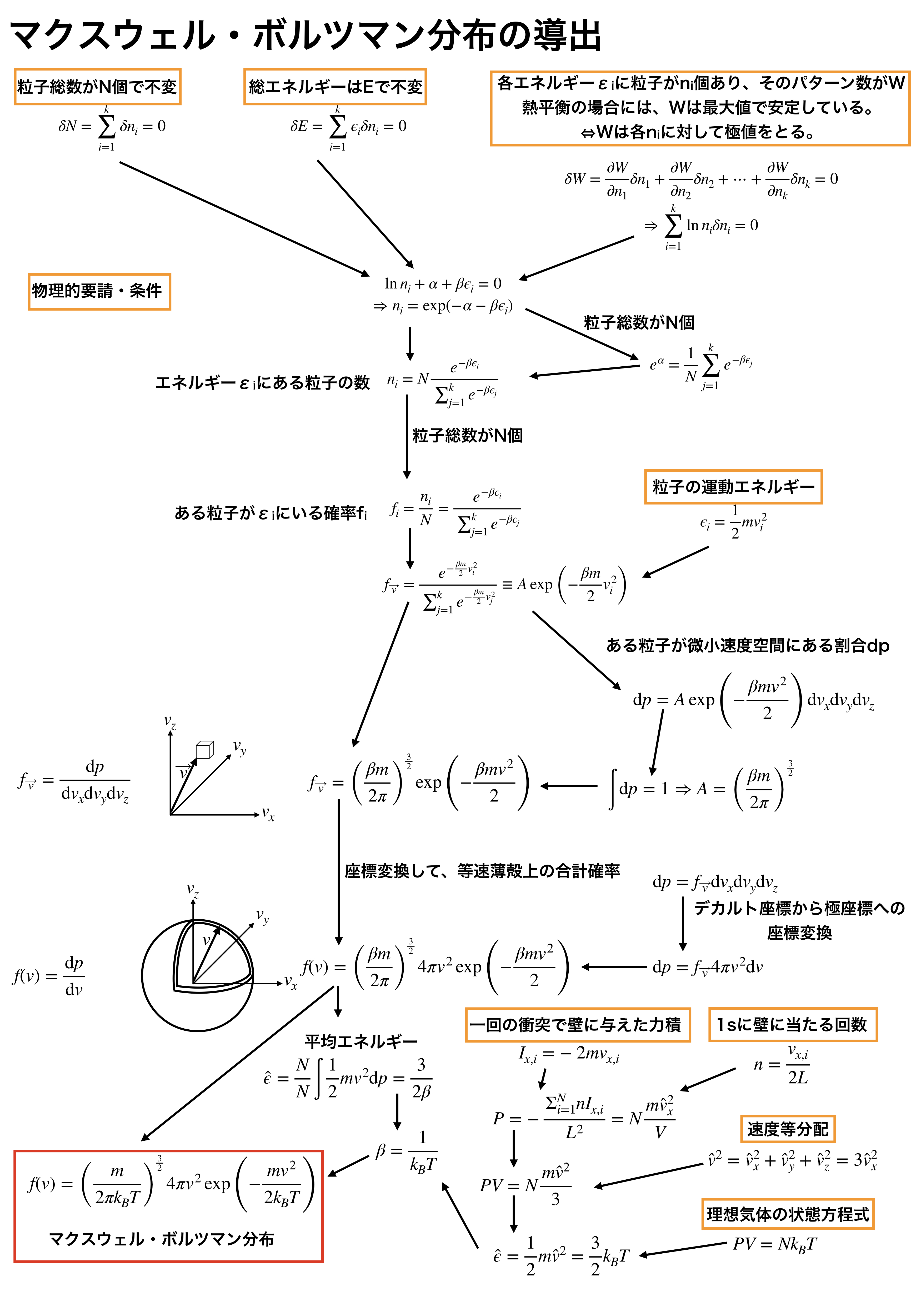
数学的な式展開をほぼ省いた導出の概要が上記です。
これによって、どのような「物理」を導出に使っているかがわかるかと思います。
結構簡単な物理法則から導かれていることがわかります。
下記で導出していきます。
ある粒子がエネルギー\(\epsilon_i \) にある確率\(f_i \)
次の図のような箱(体積\( V=L^3 \) )内の質量\( m \)粒子が飛び回っている系を考えます。
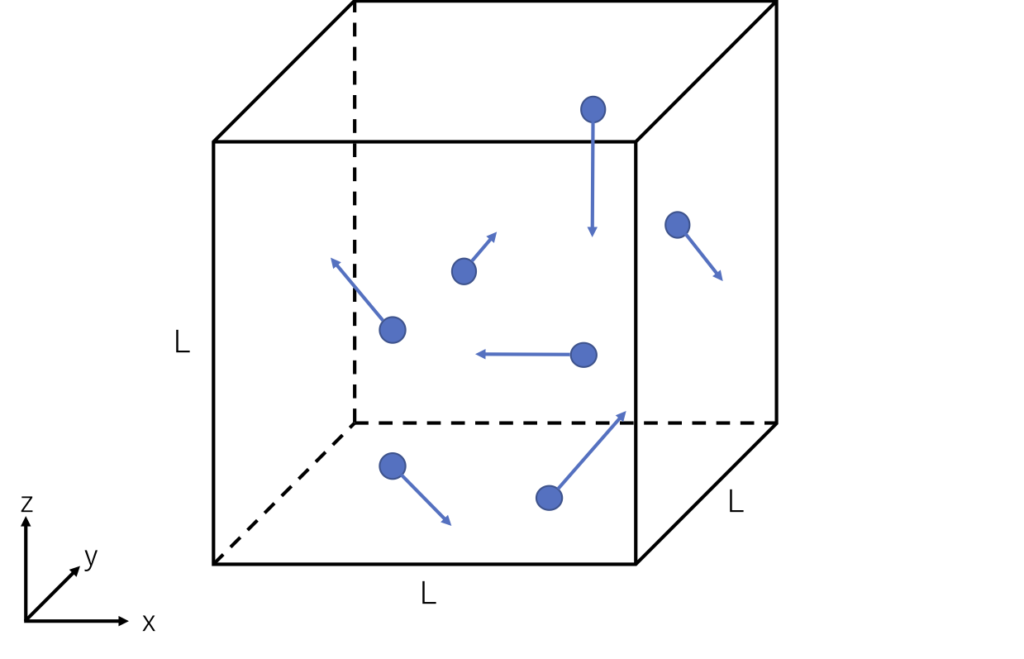
粒子たちはランダムに、各々の速度ベクトルとで飛んでいます。
まず物理的要請として3つの条件を課します。
- 粒子総数が\( N \)個で不変
$$ \delta N = \sum_{i=1}^k\delta n_i = 0 \ \ \ (eq.1)$$ - 総エネルギーが\( E \)で不変
$$ \delta E = \sum_{i=1}^k\epsilon_i\delta n_i = 0 \ \ \ (eq.2)$$ - 各エネルギー\( \epsilon_i \)には粒子が\( n_i \)個あり、その組み合わせパターン数が\( W \)
熱平衡状態を考えると\( W \)は最大値で安定している。\( \Leftrightarrow W \)は各\( n_i \)に対して極値にある。
$$ \delta W = \frac{\partial W}{\partial n_1}\delta n_1 + \frac{\partial W}{\partial n_2}\delta n_2 + \cdots + \frac{\partial W}{\partial n_k}\delta n_k = 0 \ \ \ (eq.3)$$
「組み合わせパターン数\( W \)が最大」の意味
上記の3つ目の条件が理解しづらい方もいるかと思いますので、少し物理的な意味を説明しておきます。
この条件は、「確率的に最も有り得る状態」にこの系がなっているということを意味します。
これは状態がランダムに変わり移る時、ある瞬間の観測を行った時に得られる可能性の最も高い状態を意味します。
例をあげると理解しやすいでしょう。
<例1: 2つのコイン>
2つのコインを投げた時の「確率的に最も有り得る状態」を考えてみます。
コインは表か裏(今回の系でいうエネルギー\( \epsilon_i \)の状態)しかないので、下記が全ての組み合わせパターンです。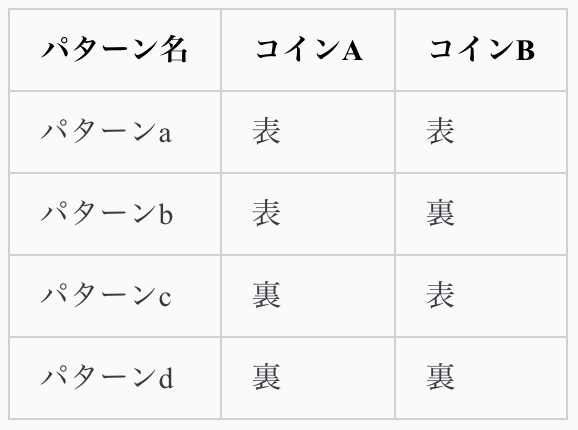
この場合の「確率的に最も有り得る状態」はパターンb, cとなる。そして、その時の系の状態は「裏が1枚、表が1枚」となる。
<例2: 3粒子が有り、全エネルギーが6の場合(エネルギーの最小単位は1)>
この場合、全ての組み合わせは粒子の名前をA, B, Cとした時に次のようになる。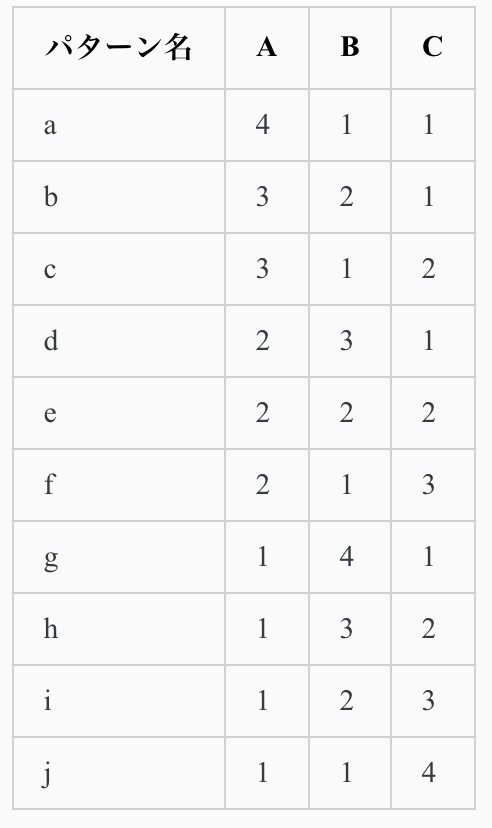
これを系の状態で書き表すと次のようにある。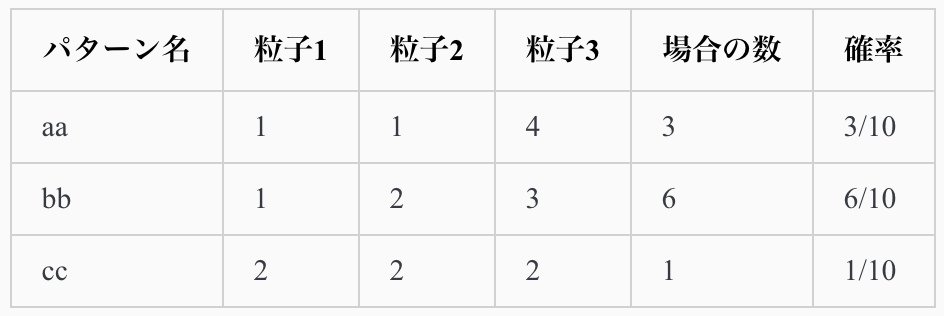
つまりこの系ではパターンbbが「確率的に最も有り得る状態」となります。
確かに、ランダムに観測を行った場合には、bbが最もたくさん観測されるだろうことは想像できます。
(eq.3)はかなり複雑な形をしているので、\( W, n_i \)が非常に大きいことを利用して近似を行います。
まず\( W \)を粒子数\( N \)と各エネルギーにある粒子数\( n_i \)で表す。
粒子が\( N \)個あり、\( k \)個のエネルギー準位に振り分けます。最初の順位へは\( n_1 \)個の粒子を振り分け、次の順位へは\( n_2 \)個振り分けていきます。
これを\( k \)回行えば良いのです。
最初の\( N \)個から\( n_1 \)個選ぶ組み合わせ\( = \)場合の数は、
$$ _NC_{n_1} = \frac{N!}{n_1(N-n_1)!} $$
です。これを繰り返していくので、掛け算されていきます。結果得られる場合の数\( W \)は、次のようになります。
$$ W = {}_NC_{n_1} \cdot {}_{(N-n_1)}C_{(N-n_1-n_2)}\cdot \cdots \cdot {}_{(N-n_1 \cdots -n_{k-1})}C_{(N-n_1-n_2 \cdots -n_k)} \\ = \frac{N!}{n_1!(N-n_1)!} \frac{(N-n_1)!}{n_2!(N-n_1-n_2)!}\cdots\frac{(N-n_1-\cdots-n_{k-1})!}{n_k!(N-n_1-n_2-\cdots-n_k)!} \\ = \frac{N!}{n_1!n_2!\cdots n_k!} \ \ \ (eq.4) $$
ここでは、\( N \)が全粒子数で、\( n_1 \)から\( n_k \)までの合計も全粒子数であることから、最後の項の分母右側は\( 0!=1 \)となります。
すると(eq.3)は次のように変形できます。
$$ \delta (\ln W) = \frac{\partial (\ln W)}{\partial n_1}\delta n_1 + \frac{\partial (\ln W)}{\partial n_2}\delta n_2 + \cdots + \frac{\partial (\ln W)}{\partial n_k}\delta n_k = 0 \\ \delta (\ln W) = \sum_{i=1}^{k} \frac{\partial (\ln W)}{\partial n_i}\delta n_i = 0 $$
ここで出てくるのが、スターリングの公式です。
スターリングの公式
$$ \ln N! = N\ln N – N $$
上記公式と(eq.4)より
$$ \ln W = \ln N! – \left( \ln n_1! + ln n_2! + \cdots + \ln n_k! \right) \\ \simeq N\ln N – N – (n_1\ln n_1 + n_2\ln n_2 + \cdots + n_k\ln n_k – n_1 – n_2 – \cdots – n_k) \\ = N\ln N – n_1\ln n_1 – n_2\ln n_2 – \cdots – n_k\ln n_k $$
であるから、
$$ \delta(\ln W) = \sum_{i=1}^k -(\ln n_i + 1)\delta n_i \\ \simeq -\sum_{i=1}^k \ln n_i \delta n_i = 0 \ \ \ (eq.5) $$
となります。
(eq.1), (eq.2), (eq.5)を全て常に満たすためには次のような条件式となります。(ラグランジュの未定係数法)
$$ \ln n_i + \alpha + \beta\epsilon_i = 0 \\ \Rightarrow n_i = \exp(-\alpha – \beta \epsilon_i) \ \ \ (eq.6) $$
総粒子数が\( N \)であるので、
$$ N = \sum_{j=1}^k n_j = \sum_{j=1}^k e^{-\alpha}e^{-\beta \epsilon_j} \\ \Rightarrow e^{\alpha} = \frac{1}{N}\sum_{j=1}^ke^{-\beta\epsilon_j} \ \ \ (eq.7) $$
(eq.6)と(eq.7)より、
$$ n_i = N\frac{e^{-\beta \epsilon_i}}{\sum_{j=1}^ke^{-\beta \epsilon_j}} \ \ \ (eq.8) $$
これがエネルギー\( \epsilon_i \)にある粒子の数となります。これを粒子の総数\( N \)で割ることで割合\( f_i \)を出すことができます。
$$ f_i = \frac{n_i}{N} = \frac{e^{-\beta \epsilon_i}}{\sum_{j=1}^ke^{-\beta \epsilon_j}} \ \ \ (eq.9) $$
これは、ある粒子がエネルギー\( \epsilon_i \)にいる確率を表しています。
速度分布関数
ここで粒子のエネルギーが運動エネルギーであるという物理的条件を課して、(eq.9)の分母を求めます。
さらに今まで「速度」で論じていたところを、座標変換して「速さ」で式を表していきます。これは、現在考えている系(多粒子で、熱平衡な系)では各粒子の飛んでいる方向とは無関係に、方向情報を含まない「速さ」のみで状態を表せるはずという考えのもとに式変形していきます。
まず、粒子のエネルギーが次のように表されるとします。
$$ \epsilon_i=\frac{1}{2}mv_i^2 $$
すると\( f_i \)は次のように書き表せます。
$$ f_{\vec{v}} = \frac{e^{-\frac{\beta m}{2} v_i^2 }}{\sum_{j=1}^ke^{-\frac{\beta m}{2}v_j^2}} \equiv A\exp\left( -\frac{\beta m}{2}v_i^2 \right) \ \ \ (eq.10) $$
ここでは、エネルギー順位\( i \)依存だった関数を、粒子の速度\( \vec{v} \)依存にしたので、添字も変えました。また複雑でよくわからない分母を1つの定数\( A \)としました。定数であることは自明ですね。
これは気体粒子の速度空間(\( v_x, v_y, v_z \) )での確率分布を意味しています。確率分布とは、注目するある粒子を適当な時刻に観測を行った時にその粒子の速度が\( v_i \)である確率を意味しています。
ある1つの気体粒子の速度空間において微小体積中(\( {\rm d}v_x{\rm d}v_y{\rm d}v_z \) )にいる確率 \( {\rm d}p \)は確率分布を使用して次のように表せます。
$$ {\rm d}p = f_{\vec{v}}{\rm d}v_x{\rm d}v_y{\rm d}v_z = A\exp \left(-\frac{\beta m v_i^2}{2} \right){\rm d}v_x{\rm d}v_y{\rm d}v_z \ \ \ (eq.11) $$
\( f_{\vec{v}} \) は確率分布であり、これに微小速度体積をかけることで、その体積内に注目する粒子がいる確率がわかるということです。
この式内の\( v_i \)はエネルギー順位が離散的な場合を考えた時の名残であるが、気体粒子を考える場合には、連続値であると仮定します。すると、気体粒子の速度空間において微小体積中の確率は次のようになります。
$$ {\rm d}p = f_{\vec{v}}{\rm d}v_x{\rm d}v_y{\rm d}v_z = A\exp \left(-\frac{\beta m v^2}{2} \right){\rm d}v_x{\rm d}v_y{\rm d}v_z \ \ \ (eq.12) $$
この式を全速度空間で積分すると、確率なので1になります。これを使って\( A \)を求めます。
$$ 1 = \int{\rm d}p = A\iiint \exp \left(-\frac{\beta m v^2}{2} \right){\rm d}v_x{\rm d}v_y{\rm d}v_z \\ = A\int_{-\infty}^\infty \exp \left(-\frac{\beta m v_x^2}{2} \right){\rm d}v_x\int_{-\infty}^\infty \exp \left(-\frac{\beta m v_y^2}{2} \right){\rm d}v_y\int_{-\infty}^\infty \exp \left(-\frac{\beta m v_z^2}{2} \right){\rm d}v_z $$
積分公式
$$ \int_{-\infty}^\infty e^{-ax^2}{\rm d}x = \sqrt{\frac{\pi}{a}} $$
を使うと、
$$ 1 = A\sqrt{\frac{2\pi}{\beta m}}\sqrt{\frac{2\pi}{\beta m}}\sqrt{\frac{2\pi}{\beta m}} $$
よって、
$$ A = \left( \frac{\beta m}{2\pi} \right)^{\frac{3}{2}} \ \ \ (eq.13) $$
と\( A \)が求まり、
$$ f_{\vec{v}} = \left( \frac{\beta m}{2\pi} \right)^{\frac{3}{2}}\exp \left(-\frac{\beta m v^2}{2} \right) \ \ \ (eq.14) $$
であることがわかります。
イメージ図として次のようになります。
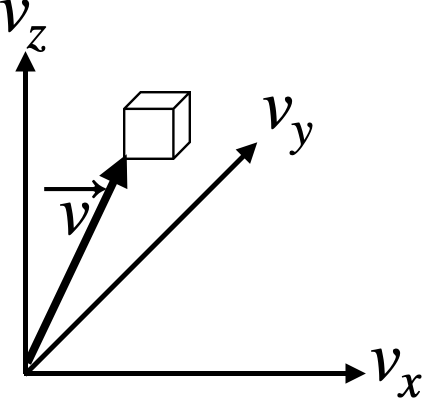
$$ f_{\vec{v}}=\frac{{\rm d}p}{{\rm d}v_x{\rm d}v_y{\rm d}v_z} $$
ここではまだ速度の方向依存性は残しているが、多粒子で熱平衡系を考えているので、等方性を仮定して、状態は「速度」ではなく、「速さ」にのみ依存すると考えますと、次のような座標変換ができます。
$$ {\rm d}p = f_{\vec{v}}{\rm d}v_x{\rm d}v_y{\rm d}v_z \Rightarrow {\rm d}p = f_{\vec{v}}4\pi v^2 {\rm d}v $$
ここで\( {\rm d}v \)は速さの微小変化量を表しており、速さはもちろん0から無限大の領域をとります。(速度、例えば\( v_x \)の場合には負の無限大から正の無限大まで取っていました。)この\( f_{\vec{v}}4\pi v^2 \)を速さ\( v \)にのみ依存する新たな関数\( f(v) \)を定義しなおすと下記になります。
$$ f(v) = \left( \frac{\beta m}{2\pi} \right)^{\frac{3}{2}}4\pi v^2\exp \left(-\frac{\beta m v^2}{2} \right) \ \ \ (eq.15) $$
これが後々マクスウェル分布となっていきます。
イメージとしては次のようになります。
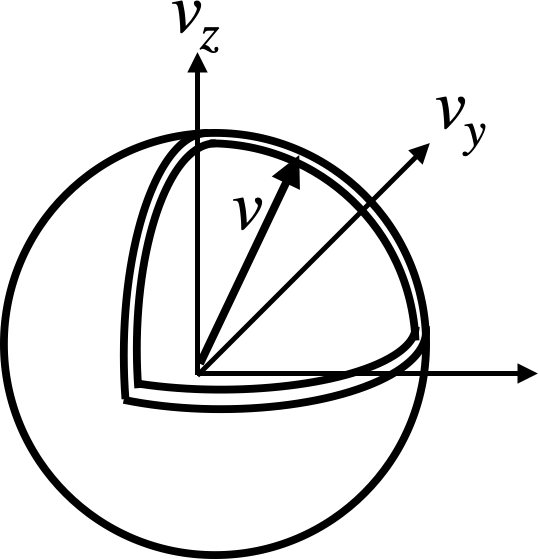
$$ f(v)=\frac{{\rm d}p}{{\rm d}v} $$
(eq.14)と(eq.15)は同じ意味を表していますが、表現が少し違います。物理的なイメージとしては、(eq.14)に等方性を仮定して極座標変換し、等速薄殻上の確率を合計したものが(eq.15)と考えれば良いと思います。
これで速度分布関数の形は決まりましたが、定数\( \beta \)がまだ定まっていません。
気体粒子論と状態方程式から\( \beta \)を求める
定数\( \beta \)を求めるために気体粒子が外壁に力積を与えるという描像を考え、さらに理想気体の状態方程式を導入する。
気体粒子\( i \)は質量\( m \)を持ち、空間を\( \vec{v}_i \) で飛んでいるとします。 この時のある一つの軸(\( x \)軸とする)に対する運動量\( p{x,i} \) は次のように表せます。
$$ p_{x,i} = mv_{x,i} $$
これが\( x \)軸に垂直な壁に全反射( \( v_{x,i} \) が \( -v_{x,i} \)になる)すると、一回の衝突で壁に与えた力積 \( I_{x,i} \) は、
$$ I_{x,i} = -mv_{x,i} – mv_{x,i} = -2mv_{x,i} $$
となります。
この粒子が単位時間\( 1[{\rm s}] \)に壁に当たる回数\( n \)は、空間の大きさが\( L \)なので、
$$ n= \frac{v_{x,i}}{2L} $$
となります。上の2式からこの粒子\( i \)が単位時間に壁に与える力積(=力\( F_{x,i} \) )が次のように計算されます。
$$ F_{x,i} = I_{x,i}n = -\frac{mv_{x,i}^2}{L} $$
では次に粒子が壁に与える圧力\( P \) (壁が全ての粒子からの合計として受け取る圧力の符号反転)を計算します。
$$ P = -\frac{\sum_{i=1}^NF_{x,i}}{L^2} =\sum_{i=1}^N\frac{mv_{x,i}^2}{L^3} \\ =\frac{mN}{L^3}\sum_{i=1}^N \frac{v_{x,i}^2}{N} =N\frac{m\hat{v}_x^2}{V} $$
速度等分配(エネルギー等分配則)
$$ \hat{v}^2=\hat{v}_x^2+\hat{v}_y^2+\hat{v}_z^2 = 3\hat{v}_x^2 $$
を考えると、次のように書き換えられます。
$$ PV=N\frac{m\hat{v}^2}{3} $$
この左辺はまさに状態方程式なので、状態方程式を導入します。
状態方程式
$$ PV=Nk_BT $$
と比較すると粒子の平均運動エネルギー\( \hat{\epsilon} \)は次のようになります。
$$ \hat{\epsilon}=\frac{1}{2}m\hat{v}^2=\frac{3}{2}k_BT \ \ \ (eq.16) $$
一方で(eq.15)の\( f(v) \)からも次のように\( \hat{\epsilon} \)が求まります。
$$ \hat{\epsilon}=\frac{N}{N}\int\frac{1}{2}mv^2{\rm d}p = \frac{N}{N}\int_0^{\infty}\frac{1}{2}mv^2f(v){\rm d}v \\ = \frac{1}{2}m\left( \frac{\beta m}{2\pi} \right)^{\frac{3}{2}} 4\pi\int_0^\infty v^4\exp\left( -\frac{\beta m}{2} v^2 \right){\rm d}v \\ = \frac{1}{2}m\left( \frac{\beta m}{2\pi} \right)^{\frac{3}{2}} 4\pi\frac{3}{8}\sqrt{\pi\left( \frac{2}{\beta m} \right)^5} \ =\frac{3}{2\beta} \ \ \ (eq.17) $$
ここでは積分公式
$$ \int_0^\infty v^4\exp(-\alpha v^2){\rm d}v = \frac{3}{8}\sqrt{\frac{\pi}{\alpha^5}} $$
を利用しました。
(eq.16)と(eq.17)より、
$$ \beta=\frac{1}{k_BT} $$
であることがわかります。
これによってやっとマクスウェル分布が次のように求まりました。
$$ f(v) = \left( \frac{m}{2\pi k_BT} \right)^{\frac{3}{2}}4\pi v^2\exp \left(-\frac{m v^2}{2k_BT} \right) $$
最後にこの関数のplotを載せます。\( m \)は窒素分子の質量を代入。
感想
今回はマクスウェル分布を導出しました。
ネットでこれを調べると案外にも最初から最後まで導入しているものがなかなか見つかりませんでした。
実際に導出してみますと、案外にも簡単な物理的要請や法則、条件から導けました。
実は本当は黒体輻射(プランクの公式など)について導出・まとめをしようと思っていましたが、辿り辿ってマクスウェル分布まで遡ってしまいました。
あとはこれを電磁波に展開させて、量子化してあげて、いろいろ式展開していけば、プランクの公式から芋づる式にレイリー・ジーンズ、ヴィーン、シュテファン・ボルツマン、などなどが導けるはず?
まぁおいおい。。。




















コメント