目次
概要
fortranで複素数を使うには次のように宣言と代入をすれば良い。
|
1 2 |
COMPLEX a a=(3.0,4.0) !(実部, 虚部) |
背景
物理、天文学という古くからある分野に関わっていると、fortranが第一プログラミング言語という人も多い。
私もその中の一人で、社会に出てみると、まるで古典文学を書く人という扱いを同僚からうける。
しかし、fortranはまだ大活躍中の言語であり、スーパーコンピュータでの配列計算にはよく使われる言語である。
今回は虚数の使い方について記す。メモがわりに。
自然界に虚数は存在しない、少なくとも人間には観測できない。しかし我々は、その存在を許さない限り自然を説明できない。
実数を観測して、虚数を「見る」ことが多い。面白い。
実例
下記のコード例に複素数で重要な点を示した。
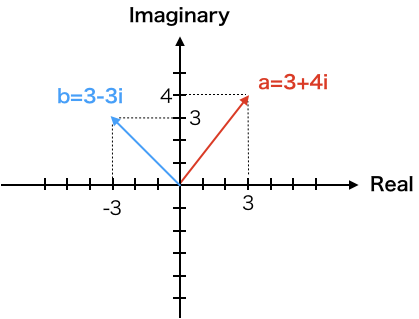
コード例内で例示している2つの虚数\( a, b\)を複素平面に示しておく。
<complex.f90>
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
PROGRAM COMPLEX IMPLICIT NONE !未宣言の変数を拒否するいつもの文言 COMPLEX a, b !複素数の変数としてa, bを宣言 REAL pi !円周率π用変数の宣言 pi=4.0*atan(1.0) !円周率をpiに代入。arctanを利用したこの書き方はよく使われる。 !複素数値の代入と、基本的な演算 a=(3.0,4.0) !複素数aを定義。a = 3 + 4i PRINT *, ABS(a) !絶対値 -> 5.00000000 PRINT *, AIMAG(a) !虚部 -> 4.00000000 PRINT *, REAL(a) !実部 -> 3.00000000 !偏角の計算 b=(-3.0, 3.0) PRINT *, ATAN2(AIMAG(b), REAL(b))/pi*180.0 !偏角 -> 135.000000 END PROGRAM COMPLEX |
上記を実行すると、下記のような出力が得られる。
|
1 2 3 4 |
5.00000000 4.00000000 3.00000000 135.000000 |
このようにして、複素数の宣言と絶対値、虚部、実部の計算がされる。さらに、偏角の計算も示した。
一応偏角\(\theta\)の計算は下記に示しておく。
$$ a=a_r + a_i i \\ \Rightarrow \tan(\theta) = \frac{a_i}{a_r} \\ \Rightarrow \theta = \arctan\left(\frac{a_i}{a_r}\right) $$
もちろん、上記の式で得られる\(\theta\)はradで表されている。
上のコード上ではradから度に単位変換している。
コメント